コブ・ダグラス生産関数は、生産高と生産投入(要因)の関係をモデル化したものである。 効率的な生産を行うための投入量の比率を計算したり、生産方式の技術的変化を推定するのに使われる。 コブ・ダグラス生産関数の一般的な形式は以下の通り。ここで、⊖(Y) は出力、⊖(x_{i}) は入力、⊖(y) は生産の全体効率と入力量の変化に対する出力の応答性を決めるパラメータである。 この関数形式が生産の測定に応用されたのは、数学者のCharles Cobbと経済学者のPaul Douglasが、1899年から1922年のアメリカの製造業の生産における労働と資本という2つの入力要素の相対的重要性を検討するためにこの関数形式を使用したからである。 CobbとDouglasのオリジナルモデルでは、生産弾力性パラメータ⊖(\alpha_{1}⊖) ⊖(\alpha_{2}⊖)を、規模への定帰還を意味する範囲㈰(0,1↩)と和を1へ制限している。 この関数はこうである。ここで、∕(x_{1}) と∕(x_{2}) はそれぞれ労働と資本を表す。 両辺の自然対数をとると、生産高、労働、資本のデータに対して、パラメータⒶ(ⒶgammaⒶ)、Ⓑ(ⒷalphaⒶ)は最小二乗法を用いて推定することができる。 CobbとDouglasのデータによると、この期間の米国の製造業生産額のうち労働が4分の3を占めている(残りの4分の1は資本が占めている)ことを意味し、”heavior “の値は0.75となる。 効率性パラメーターは1.01であり、1より大きいため、労働と資本の組み合わせによる生産に対する観測できない力の正の効果を反映している。
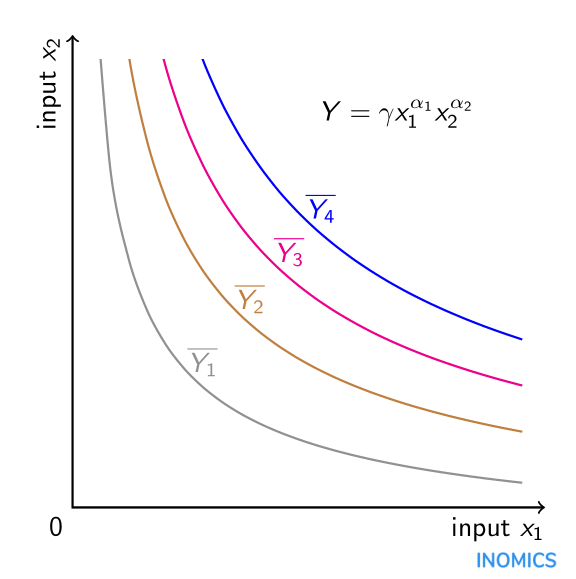
コブ・ダグラス生産関数の乗法的性質は、閾値を正として、生産において投入物が補完的であることを意味する。 標準的な労働と資本のモデルでは、資本を増やすと直接的に生産が増加するだけでなく、労働の生産性に影響を与えることで間接的にも生産が増加する。 数学的には、生産量(Y)の労働(x_{1})と資本(x_{2})に関する交差偏微分は正である。 また、生産量の労働に関する2階偏微分と資本に関する2階偏微分はともに負であり、それぞれの投入量だけでは限界収穫量が逓減していることがわかる。 労働を増やすか資本を増やすか(両方はできない)だけで、生産量は逓減しながらも増加する。 さらに、入力間の代替弾力性は、関数形式により一定で1に等しい。 2入力のCobb-Douglas生産関数は、生産高が一定となる両入力の組み合わせである等値線の形で図式化できる。 このグラフでは、(出力が一定の)出力レベルに対して、4つのisoquantsがあります。 原点から等積が離れるほど、出力のレベルも大きくなる \(\overline{Y_{4}}>overline{Y_{3}}>overline{Y_{2}}>overline{Y_{1}} )。 入力の組み合わせは、生産者が利用できる予算と、等コスト線(代替弾力性の記事参照)の形でグラフに含めることができる、入力 \(x_{1}) と入力 \(x_{2}) のコスト比によって決定されます。
CobbとDouglas自身も、彼らの生産関数が確固たる理論基盤に基づくものではなく、生産法則として理解されるべきものではなく、生産の入力と出力との観察結果の統計的近似に過ぎないと認めている。 それにもかかわらず、その単純な数学的特性は経済学者にとって魅力的であり、過去 1 世紀にわたってミクロ経済学の理論の標準となりました。
さらに読む:
背景と Cobb-Douglas 生産関数の主要特性の概要については、特に Cobb と Douglas の元の論文 “A Theory of Production” (The American Economic Review, 1928) の 6、7 および 8 節を見てください。
Good to know:
コブ・ダグラス関数形は生産理論で用いられるだけでなく、ミクロ経済学の消費者理論でも標準的に用いられており、効用関数として適用され、効用について \(Y**) が \(U**) となる。 このとき、(x_{i}) は消費項目を表し、効用関数が予算制約の下で最大化されるとき、(x_{i}) の値は個人が項目間でどのように最適に予算を配分するかを示す
。