このセクションでは、二次方程式のルートの見つけ方について学びます。 根はx-切片またはゼロとも呼ばれます。 二次関数は、原点、x軸の下、またはx軸の上にある頂点を持つ放物線でグラフ化されます。 したがって、2次関数は1つ、2つ、またはゼロの根を持つことがあります。
二次方程式を解くように言われたとき、私たちは本当は根を見つけるように言われているのです。 平方完成が二次方程式を解くのに便利な方法であることは、すでに見てきました。 この方法は、二次方程式を解くのに使われる二次式の公式を導き出すのに利用できます。 実際、関数、
f (x) = ax2 + bx + c
の根は、2次式で与えられます。 関数の根は x-切片です。 定義によれば、x軸に横たわる点のy座標は0である。 したがって、二次関数の根を見つけるには、f (x) = 0 とし、方程式、
ax2 + bx + c = 0 を解きます。
We can do this by completing the square as,
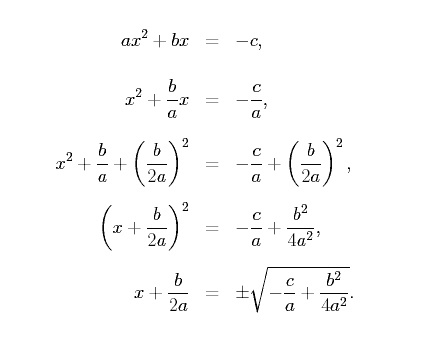
Solving for x and simplifying we have,
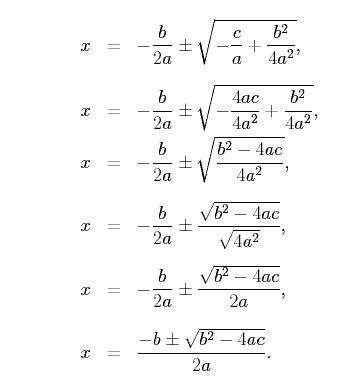
Thus, the roots of a quadratic function are given by,
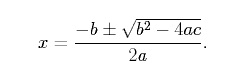
This formula is called the quadratic formula, and its derivation is included so that you can see where it comes from. We call the term b2 −4ac the discriminant. The discriminant is important because it tells you how many roots a quadratic function has. Specifically, if
1. b2 −4ac < 0 There are no real roots.
2. b2 −4ac = 0 There is one real root.
3. b2 −4ac > 0 There are two real roots.
We will examine each case individually.
ケース 1: 実根がない
二次関数の判別式が 0 より小さい場合、その関数には実根がなく、それが表す放物線は x 軸に交差しません。 二次式では判別式の平方根を取る必要があるので、負の数の平方根は実線上で定義されないため、判別式が負になると問題が生じます。 実根を持たない二次関数の例として、
f(x) = x2 – 3x + 4 があります。
f(x) の判別式が負であることに注意してください。
b2 -4ac = (-3)2- 4 – 1 – 4 = 9 – 16 = -7 です。
この関数は、頂点が x 軸の上にある、上に開く放物線で表されます。
ケース 2: 1 つの実根
二次関数の判別式が 0 に等しければ、その関数はちょうど 1 つの実根を持ち、1 つの点で x 軸を横切ることがあります。 これを見るために、二次式の b2 -4ac = 0 とすると、
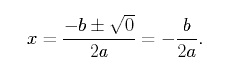
が放物線の頂点の X 座標であることに注意してください。 このように、放物線の頂点がx軸上にあるとき、放物線はちょうど1つの実根を持つことになります。 実根が 1 つしかない 2 次関数の最も単純な例は、
y = x2,
ここで、実根は x = 0 です。
実根が 1 つの 2 次関数の別の例は、
f(x) = -4×2 + 12x – 9 で与えられます。
f(x) の判別式が 0 であることに注意してください。
b2 -4ac = (12)2- 4 -4 -9 = 144 – 144 = 0。
この関数は下向きに開き、x 軸上にある頂点 (3/2, 0) を持つ放物線によってグラフ化されています。 Thus, the graph intersects the x-axis at exactly one point (i.e. has one root) as shown below,
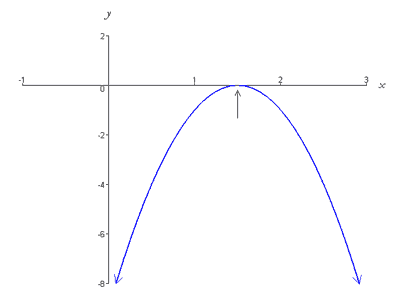
Case 3: Two Real Roots
If the discriminant of a quadratic function is greater than zero, that function has two real roots (x-intercepts). Taking the square root of a positive real number is well defined, and the two roots are given by,
An example of a quadratic function with two real roots is given by,
f(x) = 2×2− 11x + 5.
Notice that the discriminant of f(x) is greater than zero,