投影
次元削減の概念と SVD と主成分分析のアプリケーションのいくつかを説明したので、これらの背後にある数学に関連する詳細に焦点を当てます。 まず、投影から始めます。 投影は線形代数の概念であり、高次元データで実行する数学的操作の多くを理解するのに役立ちます。 詳しくは、線形代数の本でプロジェクションを復習することができる。
復習として、投影は点と部分空間の間の距離を最小化することを覚えておいてください。

上の図では、上の点は空間内の点を指しています。 この特定の漫画では、空間は 2 次元ですが、私たちは抽象的に考える必要があります。 空間は直交平面で表され、小人が立っている線は点の部分空間である。 この部分空間への投影が、元の点に最も近い場所となる。 幾何学では、点から空間に垂線(点線)を落とすことで、この最も近い点を見つけることができる。 小さな人は投影の上に立っています。
投影の説明のために、点に対する標準的な行列代数の表記法を使用します。
mypar (1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)text(2,3," Y",pos=4,cex=3)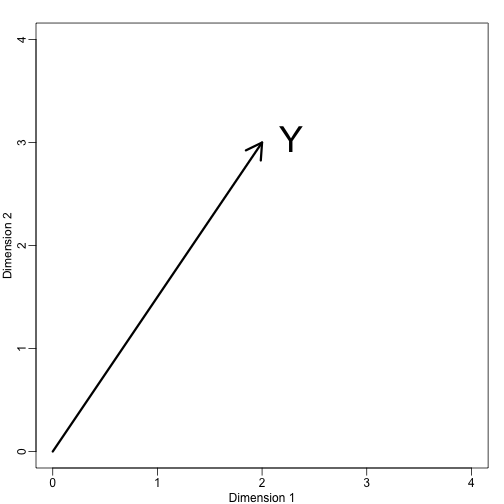
すぐに、このベクトルを、以下で定義する空間に射影して、座標系を定義することができます。 (x 軸) と (y 軸) で定義される空間に投影することで、すぐに座標系を定義できます。
これらの点によって定義される部分空間への投影はそれぞれ 2 と 3 です。
私たちは、and が座標、that が基底であると言います。 を満たす点によって定義される部分集合が、下のプロットの赤線です。 への投影は、. と. の間の距離を最小にするものを見つける必要があります。 線形代数では、これらの点間の差は空間に直交していることを学びますので、
これは、
and:
ここで、ドットは内積を表します: .
次の R コードで、この式が動作することを確認します:
mypar(1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)abline(0,0.5,col="red",lwd=3) #if x=2c and y=c then slope is 0.5 (y=0.5x)text(2,3," Y",pos=4,cex=3)y=c(2,3)x=c(2,1)cc = crossprod(x,y)/crossprod(x)segments(x*cc,x*cc,y,y,lty=2)text(x*cc,x*cc,expression(hat(Y)),pos=4,cex=3)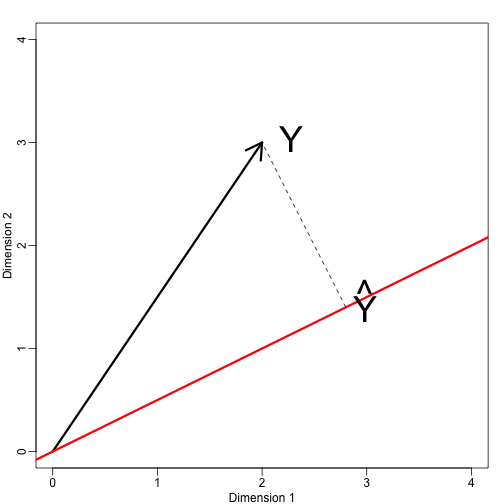
もし 、がそのようだったら、単にで空間は変化しないことに注意してください。 この単純化は、私たちが直交行列を好む理由の 1 つです。
例。
この空間では、ベクトルのすべての成分は同じ数なので、この空間は定数を表すと考えることができます:投影では、各次元は同じ値になります。
このような問題について話すとき、私たちは上のような 2 次元の図形を使うことがあります。
質問に戻ると、投影は
この場合は平均です
ここで、微積分を使用することも同じくらい簡単だったでしょう
例。 回帰は投影でもある
もう少し複雑な例を挙げましょう。 単純な線形回帰は、投影でも説明できます。 データ (もはやこの表記は使いません) は再びベクトルであり、モデルは直線で予測します。 We want to find the and that minimize the distance between and the space defined by:
with:
Our matrix is and any point in can be written as .
The equation for the multidimensional version of orthogonal projection is:
which we have seen before and gives us:
And the projection to is therefore: