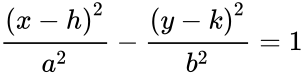by: adminPosted on:

準長軸

File:Semimajoraxis.png

楕円の半長軸

幾何学では、半長軸 (半長軸とも) という用語は、楕円や双曲線の寸法を表すのに使われます。

楕円

楕円の長軸はその最も長い直径で、中心と両方の焦点を通る線であり、その端は形状の最も幅の広い点に位置しています。

半長径は長径の半分で、中心から焦点を通って楕円の端まで伸びている。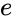{displaystyle b,\!}{displaystyle e,\!}} を通じて関係がある。} と半月状の直腸{{displaystyle ⑅︎,⑅︎!{displaystyle b=a{sqrt {1-e^{2}}},}{displaystyle \ell =a(1-e^{2})\,}{Displaystyle aell =b^{2}},\!}.

放物線は、{{displaystyle Ⓐ,Ⓑ}{{displaystyle a,\!}{displaystyle b,\!}{displaystyle a,\!} は無限遠になりにくい。

半長径とは、ある焦点から楕円上の点までの距離のうち、最も小さいものと最も大きいものの平均値です。 ここで、一方の焦点を原点に、もう一方の焦点を正のx軸に置いて、極座標で方程式を考えてみましょう

{displaystyle r(1-ecos \theta )=l,♪theta!}

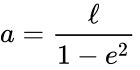
The mean value of {\displaystyle r={\ell \over {1+e}}\,\!} and {\displaystyle r={\ell \over {1-e}}\,\!}, is {\displaystyle a={\ell \over {1-e^{2}}}\,\!}.

Hyperbola

The semi-major axis of a hyperbola is one half of the distance between the two branches; if this is a in the x-direction the equation is:

{\displaystyle {\frac {\left(x-h\right)^{2}}{a^{2}}}-{\frac {\left(y-k\right)^{2}}{b^{2}}}=1}

In terms of the semi-latus rectum and the eccentricity we have

{\displaystyle a={\ell \over e^{2}-1}}

Astronomy

Orbital period

In astrodynamics the orbital period 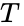{\displaystyle T\,} of a small body orbiting a central body in a circular or elliptical orbit is:

{\displaystyle T=2\pi {\sqrt {a^{3}/\mu }}}

where:

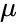
{displaystyle a,}{displaystyle \mu } は標準重力パラメータ

与えられた半長径のすべての楕円について、軌道周期は離心率とは無関係に同じになることに注意してください。

天文学では、半長軸は軌道周期と並んで、軌道の最も重要な要素の一つです。 太陽系天体の場合、半長径と軌道の周期は、ケプラーの第三法則 (元々は経験的に導かれたもの) によって関連付けられます

{displaystyle T^{2}=a^{3},}

ここで T は年単位の周期、a は天体単位の半長軸を表します。

{displaystyle T^{2}={{frac {4}pi ^{2}}{G(M+m)}}a^{3},}

ここで G は重力定数、M は中心体の質量、m は軌道上の体の質量である。 通常、中心天体の質量は周回する天体の質量よりはるかに大きいので、m は無視してもかまいません。

注目すべきは、軌道天体の重心周りの経路と、その主天体に対する経路が、両方とも楕円であることです。 天文学で使われる半長軸は、常に主から副への距離です。したがって、惑星の軌道パラメータは、天動説の言葉で与えられます。 原始軌道と絶対軌道の違いは、地球-月系を見ればよくわかる。 この場合、質量比は81.30059である。 地球-月の特性距離（地動説の月軌道の半長軸）は、384,400kmです。 一方、バリセントリックな月軌道の半長軸は379,700kmで、その差4,700kmを地球の逆軌道が担っている。 月の平均軌道速度は秒速1.010km、地球のそれは秒速0.012kmである。

平均距離

よく、半長径は主星 (楕円の焦点) と軌道上の天体の間の「平均」距離であると言われることがあります。

  • 偏心異常 (q.v.) の距離を平均すると、確かに半長径になります。
  • 真の異常 (焦点で測定された真の軌道角) を平均すると、奇妙なことに、半長径になります。 {displaystyle b=a{sqrt {1-e^{2}}},{ta!.
  • 平均異常（近点から経過した軌道周期の割合を角度で表したもの）を平均化すると、最後に時間平均（素人には「平均」が通常意味するもの）が得られます。） {displaystyle a(1+{thefrac {e^{2}}{2}})\,} です。

半径の逆数の時間平均は、{displaystyle r^{-1}},\!} となります。

Energy; calculation of semi-major axis from state vectors

天体力学では軌道の状態ベクトルから{displaystyle a,} 半長径を求めることができる。

{\displaystyle a={-\mu \over {2\epsilon }}\,} for an elliptical orbit and {\displaystyle a={\mu \over {2\epsilon }}\,} for a hyperbolic trajectory

and

{\displaystyle \epsilon ={v^{2} \over {2}}-{\mu \over \left|\mathbf {r} \right|}} (specific orbital energy)

and

{\displaystyle \mu =GM\,} (standard gravitational parameter),

where:

  • {\displaystyle v\,} is orbital velocity from velocity vector of an orbiting object,
  • {\displaystyle \mathbf {r} \,} is cartesian position vector of an orbiting object in coordinates of a reference frame with respect to which the elements of the orbit are to be calculated (e.g.
  • {displaystyle G,}は重力定数、
  • {displaystyle M}は中心天体の質量、
  • {displaystyle C,}は中心天体を表わす。

与えられた中心体と全比重エネルギーでは、偏心に関係なく、常に半長径は同じであることに注意してください。

国際宇宙ステーションの軌道周期は 91.74 分であり、したがって半長径は 6738 km となります。 軌道の長さが 300 km 増えるごとに 40 秒かかり、速度が低下するとさらに 20 秒かかります。

国際宇宙ステーションの軌道周期は 91.74 分で、半長径は 6738 km です。

コメントを残す

メールアドレスが公開されることはありません。 * が付いている欄は必須項目です