Discussion of confidence interval for \(\mu_{Y}), we used the formula to investigate what factors affect the width of confidence interval.では、信頼区間の幅に影響する要因を調べました。 もう一度やる必要はありません。
では、その代わりに、(y_{new}) の予測区間について調べてみましょう。 + \dfrac{(x_h-bar{x})^2}{sum(x_i-bar{x})^2}right)})
そして、この式は “the confidence interval for \(mu_{Y}}):
(\hat{y}_h \pm t_{(1-⑯alpha/2, n-2)}” と比較してみてください。 + \dfrac{(x_h-bar{x})^2}{sum(x_i-bar{x})^2}right)})
式の唯一の違いは、(y_{new}}の予測の標準誤差にはMSE項が追加され、(∕)の適合の標準誤差はないことであることに注意しましょう。
この余分なMSE項の原因は何なのか、予測区間を理解することにしましょう。 その際、まずは簡単な問題から始めてみましょう。 もし、”ある “場所での “新しい “応答(response)の平均値(response)が分かっていた場合、どのように予測すれば良いかを考えてみましょう。 即ち、(x_{h} = 40^{o}) Nにおける皮膚がん死亡率の平均値が150人/100万人(分散400)であることが分かっていたとしたら?
このように「 \mu_{Y} = 150 」「 \sigma^{2} = 400 」が分かっているので、「正規分布データの測定値の95%は平均から2標準偏差以内にある」という経験則を利用することができるのです。 つまり、測定値の95%は、以下の区間に含まれる、ということです。
95%ルールを適用した場合: \(\mu_{Y} = 150) and \(\sigma= 20):
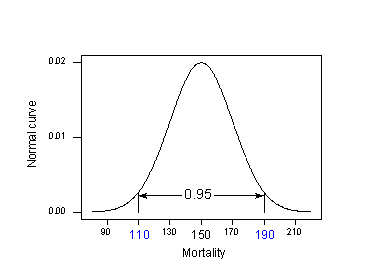
北緯40度の場所の皮膚がん死亡率の95%は、150 – 2(20) = 110と150 + 2(20) = 190で挟まれた区間にあります。
つまり、もし誰かが北緯 40 度の場所の皮膚がん死亡率を知りたければ、我々の最良の推測は 1,000 万人あたりの死亡数が 110 と 190 の間のどこかであろうということです。 問題は、この計算には、通常では知り得ない母集団の値である「閾値」と「閾値」を使っていることです。 Reality sets in:
- 平均値 \(\mu_{Y}) は一般的に知られていない。 論理的には、予測された反応であるㄧ(ㄧhat{y}) でそれを推定することになります。 \hat{y}} を使って \(\mu_{Y}}) を推定するコストは、 \(\hat{y}) の分散です。 つまり、サンプルが違えば予測値も違ってくるので、この分散を考慮しなければならないのです。
これらの未知量を推定する必要があるため、新しい反応の予測の変動は2つの要素に依存します。
- the variation due to estimating the mean \(\mu_{Y}) with \(\hat{y}_h) , which shows “\(sigma^2(\hat{Y}_h)\)”.この量の推定値は信頼区間の式に現れる適合度の標準誤差の二乗であることに注意してください)
- 応答yの変動量、これを” \(sigma^2) “と表記しています。「
2つの分散成分を足すと、
(\sigma^2+sigma^2(\hat{Y}_h)\)
は次のように推定されます:
MSE+MSE \left( + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \right) =MSEleft( 1+Âdfrac{1}{n}) + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \୧⃛(๑⃙⃘◡̈๑⃙⃘)୨⃛この量に見覚えがありますか? 予測区間の式に出てくる予測値の分散です!
もう一度2つの区間を比べてみましょう:
Confidence interval for \(mu_{Y}}colon \hat{y}_h t_{(1-ÁLPHA/2, n-2)}}
Confidence interval for \(y_{new})}{p>{mu_{Y}}Cononcon|{p>{mu_{new}}t_pm t_{(1-ÁLPHA/2, n-2)}}
Prediction interval for \(y_{new}colon \hat{y}_h t_{(1-ÄTHALpha/2, n-2)}} {Prediction interval for y_{new}Container} {Prediction interval for \{premium} {premium}}} {Prediction interval for y_{new}Container} {premium}} {Premium}}
div + \frac{(x_h-bar{x})^2}{sum(x_i-bar{x})^2}right)})
二つの公式の違いで実用上どのような影響がありますか。
- 予測区間にはMSE項が追加されるため、 \(x_{h}) における \(mu_{Y}) の信頼区間は、対応する \(x_{h}) における \(y_{new}) の予測区間より常に狭くなります。
- 予測値の標本平均での区間を計算し、サンプルサイズnを大きくすると、信頼区間の標準誤差が0に近づくことができる。予測区間はMSE項が余分にあるため、予測区間の標準誤差を0に近づけることができない。
最初の含意は、皮膚がん死亡率の例について、次のプロットを研究することによって最も簡単にわかります。
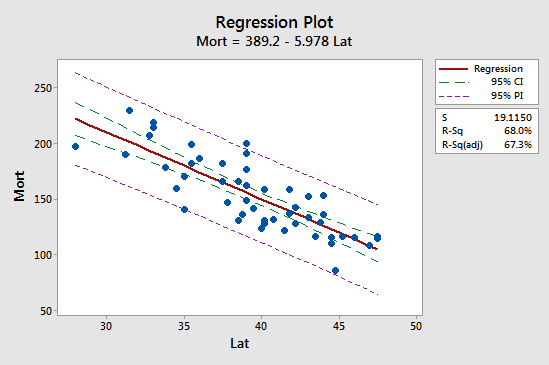
予測間隔 (95% PI、紫) が信頼間隔 (95% CI、緑) より常に広いことを観察してください。 さらに、両方の区間は、予測値の平均(約39.5)で最も狭くなっています。