Na nossa discussão sobre o intervalo de confiança para \i_(\i_{Y}}), usamos a fórmula para investigar quais fatores afetam a largura do intervalo de confiança. Não há necessidade de fazer isso novamente. Como as fórmulas são tão similares, acontece que os fatores que afetam a largura do intervalo de previsão são idênticos aos fatores que afetam a largura do intervalo de confiança.
Vamos investigar a fórmula do intervalo de previsão para \(y_{new}}):
(que{y}_h {(1-\a/2, n-2)} \vezesqrt (MSE) vezes esquerda (1+dfrac) (1) +dfrac{(x_h-h-bar{x})^2}{sum(x_i-i-bar{x})^2}})
p> para ver como se compara à fórmula do intervalo de confiança para {mu_{Y}:p>(o que{y}_h {(1-alpha/2, n-2)} \vezesqrt{MSE esquerda{1}{n} +dfrac{(x_h-h-bar{x})^2}{sum(x_i-bar{x})^2}})
Observar que a única diferença nas fórmulas é que o erro padrão da previsão para {y_{new}} tem um termo MSE extra que o erro padrão do ajuste para {mu_{Y}) não tem.
Tentemos entender o intervalo de previsão para ver o que causa o termo MSE extra. Ao fazer isso, vamos começar com um problema mais fácil primeiro. Pense em como poderíamos prever uma nova resposta a um determinado problema, se a média das respostas fosse conhecida. Ou seja, suponhamos que se soubesse que a mortalidade média do cancro de pele a 40^ N é de 150 mortes por milhão (com uma variação de 400)? Qual é a mortalidade prevista de câncer de pele em Columbus, Ohio?
p>Porque \(\mu_{Y} = 150 \) e \( \sigma^{2} = 400 \) são conhecidas, podemos tirar vantagem da “regra empírica”, que afirma entre outras coisas que 95% das medidas dos dados normalmente distribuídos estão dentro de 2 desvios padrão da média. Ou seja, diz que 95% das medidas estão no intervalo ensanduichado por:
(mu_{Y}- 2\sigma} e {mu_{Y}+ 2\sigma}.
Aplicando a regra dos 95% ao nosso exemplo com {\i1}(mu_{\i} = 150\i} e {\i1}(Sigma= 20\i}):
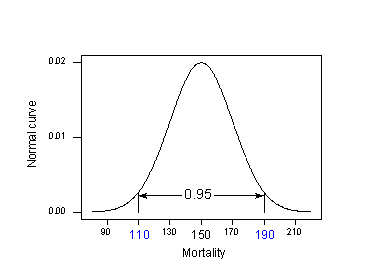
95% das taxas de mortalidade por câncer de pele de locais a 40 graus de latitude norte estão no intervalo ensanduichado por:
150 – 2(20) = 110 e 150 + 2(20) = 190.
Isto é, se alguém quisesse saber a taxa de mortalidade por câncer de pele de um local a 40 graus norte, nosso melhor palpite seria algo entre 110 e 190 mortes por 10 milhões. O problema é que o nosso cálculo usou valores populacionais que normalmente não saberíamos. A realidade se estabelece em:
- A média {\mu_{Y}) não é tipicamente conhecida. A coisa lógica a fazer é estimá-la com a resposta prevista. O custo de usar a resposta prevista para estimar é a variação da resposta prevista. Ou seja, amostras diferentes produziriam previsões diferentes, e por isso temos de ter em conta esta variância de A coisa lógica a fazer é estimá-la com MSE.
Porque temos de estimar estas quantidades desconhecidas, a variação na previsão de uma nova resposta depende de dois componentes:
- a variação devida a estimar a média {(mu_{Y}) com {hat{y}_h}, que denotemos “{sigma^2({Y}_h)}.”(Note que a estimativa desta quantidade é apenas o quadrado do erro padrão do ajuste que aparece na fórmula de intervalo de confiança.)
a variação nas respostas y, que nós denotemos como “\i^2”.”(Note que a quantidade é estimada, como de costume, com o erro quadrado médio MSE.)
Adicionando os dois componentes da variância, obtemos:
p>(\sigma^2+\sigma^2(\sigma^2+\sigma^2(que{Y}_h)})p>que é estimado por:p>(MSE+MSE \esquerda( \dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \direita) =MSE esquerda( 1+dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \i1) \i1)
Reconhece esta quantidade? É apenas a variação da previsão que aparece na fórmula para o intervalo de previsão {y_{new}}!
P>Vamos comparar novamente os dois intervalos:
Intervalo de confiança para o intervalo de previsão {mu_{Y}_h {y}_pm t_{(1-alpha/2, n-2)} \vezesqrt{MSE {MSE {1}esquerda(frac{1}n} +frac{(x_h-h-bar{x})^2}{sum(x_i-i-bar{x})^2})^2})
p> Quais são as implicações práticas da diferença entre as duas fórmulas?Porque o intervalo de previsão tem o termo MSE extra, um intervalo de confiança de 100% para a(y_mu_{Y}) à(x_h) será sempre mais estreito do que o correspondente intervalo de previsão de 100% para a(y_new) à(x_h).
A primeira implicação é vista mais facilmente estudando o seguinte gráfico para o nosso exemplo de mortalidade por câncer de pele:
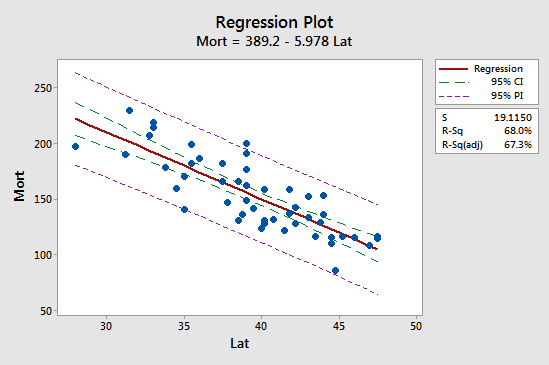
Observe que o intervalo de previsão (95% PI, em roxo) é sempre maior do que o intervalo de confiança (95% CI, em verde). Além disso, ambos os intervalos são mais estreitos na média dos valores preditores (cerca de 39,5).