Nesta seção, aprenderemos como encontrar a(s) raiz(s) de uma equação quadrática. Raízes também são chamadas de x-intercepções ou zeros. Uma função quadrática é representada graficamente por uma parábola com vértice localizado na origem, abaixo do eixo x, ou acima do eixo x. Portanto, uma função quadrática pode ter uma, duas, ou zero raízes.
Quando nos é pedido que resolvamos uma equação quadrática, estamos realmente a ser solicitados a encontrar as raízes. Nós já vimos que completar o quadrado é um método útil para resolver equações quadráticas. Este método pode ser usado para derivar a fórmula quadrática, que é usada para resolver equações quadráticas. Na verdade, as raízes da função,
f (x) = ax2 + bx + c
são dadas pela fórmula quadrática. As raízes de uma função são os interceptores x. Por definição, a coordenada y dos pontos que se encontram no eixo x é zero. Portanto, para encontrar as raízes de uma função quadrática, definimos f (x) = 0, e resolvemos a equação,
ax2 + bx + c = 0.
We can do this by completing the square as,
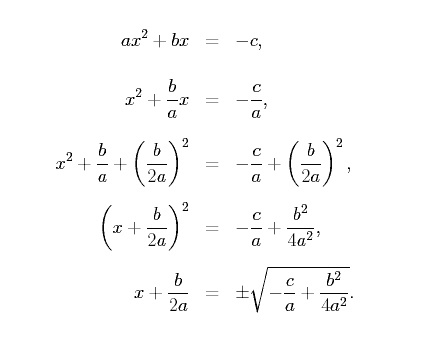
Solving for x and simplifying we have,
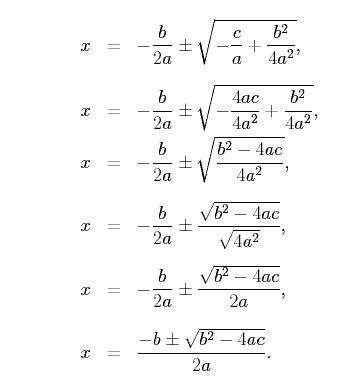
Thus, the roots of a quadratic function are given by,
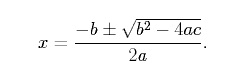
This formula is called the quadratic formula, and its derivation is included so that you can see where it comes from. We call the term b2 −4ac the discriminant. The discriminant is important because it tells you how many roots a quadratic function has. Specifically, if
1. b2 −4ac < 0 There are no real roots.
2. b2 −4ac = 0 There is one real root.
3. b2 −4ac > 0 There are two real roots.
We will examine each case individually.
Caso 1: Sem Raízes Reais
Se o discriminante de uma função quadrática for inferior a zero, essa função não tem raízes reais, e a parábola que representa não intercepta o eixo x. Uma vez que a fórmula quadrática requer tomar a raiz quadrada do discriminante, um discriminante negativo cria um problema porque a raiz quadrada de um número negativo não é definida sobre a linha real. Um exemplo de uma função quadrática sem raízes reais é dado por,
f(x) = x2 – 3x + 4.
Nota que o discriminante de f(x) é negativo,
b2 -4ac = (-3)2- 4 – 1 – 4 = 9 – 16 = -7.
Esta função é representada graficamente por uma parábola que se abre para cima cujo vértice está acima do eixo x. Assim, o gráfico nunca pode intersectar o eixo x e não tem raízes, como mostrado abaixo,
Case 2: One Real Root
Se o discriminante de uma função quadrática for igual a zero, essa função tem exatamente uma raiz real e cruza o eixo x em um único ponto. Para ver isto, definimos b2 -4ac = 0 na fórmula quadrática para obter,
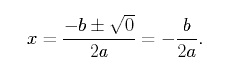
Note que 
é a coordenada x do vértice de uma parábola. Assim, uma parábola tem exatamente uma raiz real quando o vértice da parábola está bem no eixo x. O exemplo mais simples de uma função quadrática que tem apenas uma raiz real é,
y = x2,
onde a raiz real é x = 0.
Outro exemplo de uma função quadrática com uma raiz real é dado por,
f(x) = -4×2 + 12x – 9.
Note que o discriminante de f(x) é zero,
b2 -4ac = (12)2- 4 – -4 – -9 = 144 – 144 = 0.
Esta função é graficamente representada por uma parábola que abre para baixo e tem vértice (3/2, 0), deitado no eixo x. Thus, the graph intersects the x-axis at exactly one point (i.e. has one root) as shown below,
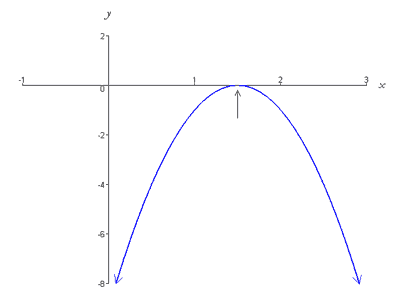
Case 3: Two Real Roots
If the discriminant of a quadratic function is greater than zero, that function has two real roots (x-intercepts). Taking the square root of a positive real number is well defined, and the two roots are given by,
An example of a quadratic function with two real roots is given by,
f(x) = 2×2− 11x + 5.
Notice that the discriminant of f(x) is greater than zero,