A função de produção Cobb-Douglas modela a relação entre a produção e os inputs (factores) de produção. É utilizada para calcular as relações entre os inputs para uma produção eficiente e para estimar a mudança tecnológica nos métodos de produção. A forma geral de uma função de produção Cobb-Douglas para um conjunto de inputs é onde Y significa output, x significa input e gamma e alfa são parâmetros que determinam a eficiência global da produção e a capacidade de resposta do output a mudanças nas quantidades de inputs. A aplicação desta forma funcional na medição da produção deve-se ao matemático Charles Cobb e ao economista Paul Douglas, que a utilizaram para considerar a importância relativa dos dois fatores de entrada, trabalho e capital, na produção industrial nos EUA no período de 1899 a 1922. Em seu modelo original, Cobb e Douglas restringem os parâmetros de elasticidade de saída (alfa_{1}) e (alfa_{2}) à faixa de variação (alfa_i) à esquerda (0,1 direita) e à soma a um, o que implica retornos constantes à escala. A função é, portanto, onde o trabalho e o capital representam, respectivamente, o trabalho e o capital. Tomando o logaritmo natural de ambos os lados da equação, os rendimentos, de tal forma que para os dados sobre a produção, o trabalho e o capital, os parâmetros (gamma) e (alfa_{1}) podem ser estimados usando os Mínimos Quadrados Ordinários. Com base em seus dados, Cobb e Douglas encontram um valor de 0,75 para {1}(alfa_{1}), o que implica que a mão de obra representou três quartos do valor da produção industrial norte-americana (capital contábil para o trimestre restante) durante o período estudado. A sua estimativa para o parâmetro de eficiência \i(\gamma) é 1,01, o que, sendo superior a 1, reflete os efeitos positivos de forças não observáveis na produção através da combinação de trabalho e capital.
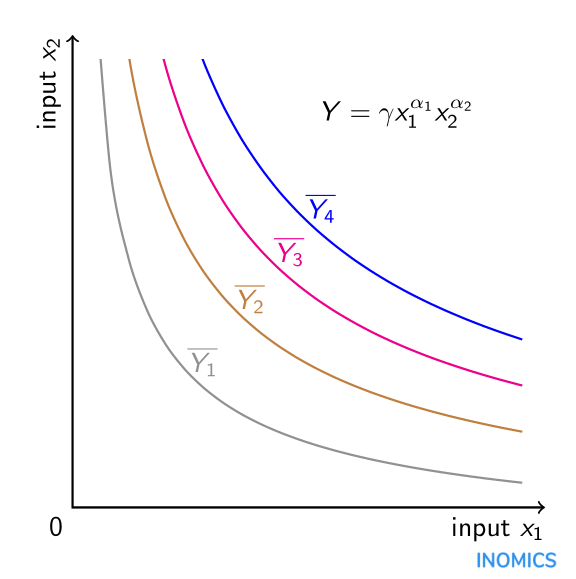
A natureza multiplicativa de uma função de produção Cobb-Douglas, assumindo valores positivos para \i(\alfa_{i}}), significa que os insumos são complementos na produção. No modelo standard de trabalho e capital, o aumento da quantidade de capital aumenta a produção não só directamente, mas também indirectamente através do seu impacto na produtividade do trabalho. Matematicamente, a derivada parcial cruzada do produto da produção (Y) com respeito ao trabalho (x_{1}}) e ao capital (x_{2}) é positiva. Além disso, devido ao pressuposto de que os derivados parciais de segunda ordem do produto da produção em relação ao trabalho e em relação ao capital são ambos negativos, implicando uma diminuição dos retornos marginais apenas para cada input. A simples adição de mais mão-de-obra ou mais capital (mas não ambos) ao processo de produção aumenta a produção, embora a uma taxa decrescente. Além disso, a elasticidade de substituição entre os inputs é constante e igual a um devido à forma funcional. Uma função de produção Cobb-Douglas de dois inputs pode ser representada graficamente na forma de isoquants: combinações de ambos os inputs para as quais o output é constante. Há quatro isoquantas no gráfico aqui para os níveis de saída (constantes) (sobre-linha{Y_{1}}), (sobre-linha{Y_{2}), (sobre-linha{Y_{3}) e (sobre-linha{Y_{4}). Quanto mais distante a isoquantidade da origem, maior o nível de saída (Y_{4}}>\overline{Y_{3}}>\overline{Y_{2}}>\overline{Y_{1}}). A combinação precisa dos inputs (x_{1}}) e {x_{2}} que é ideal para a produção é determinada pelo orçamento disponível para o produtor, bem como pela relação custo do input (x_{2}) para o input (x_{1}) que pode ser incluída no gráfico sob a forma de uma linha de isocost (ver o artigo sobre elasticidade de substituição).
Cobb e Douglas reconheceram que a sua função de produção não assenta em bases teóricas sólidas, nem deve ser entendida como uma lei de produção; representa apenas uma aproximação estatística das relações observadas entre inputs e outputs de produção. No entanto, suas simples propriedades matemáticas são atraentes para os economistas e têm levado a se tornar um padrão na teoria microeconômica ao longo do século passado.
Outras leituras:
Para um pano de fundo e uma visão geral das principais propriedades das funções de produção da Cobb-Douglas, ver em particular as seções 6, 7 e 8 do artigo original de Cobb e Douglas, “A Theory of Production” (The American Economic Review, 1928).
Bom para saber:
A forma funcional Cobb-Douglas não só é usada na teoria da produção, mas também se tornou padrão na teoria do consumidor microeconômico, onde é aplicada como uma função de utilidade, onde se torna U(Y) para utilidade. O {\i}(x_{i}) então representa itens de consumo e, quando a função utilidade é maximizada sujeita a uma restrição orçamentária, os valores para o {\i}(alfa_{i}) indicam como o indivíduo irá distribuir o orçamento de forma otimizada entre os itens.