Projeções
Agora que descrevemos o conceito de redução de dimensão e algumas das aplicações da SVD e análise de componentes principais, concentramo-nos em mais detalhes relacionados com a matemática por detrás destas. Começamos com as projecções. Uma projeção é um conceito de álgebra linear que nos ajuda a entender muitas das operações matemáticas que realizamos em dados de alta dimensão. Para mais detalhes, você pode rever projetos em um livro de álgebra linear. Aqui fornecemos uma revisão rápida e depois fornecemos alguns exemplos relacionados à análise de dados.
Como uma revisão, lembre-se que projeções minimizam a distância entre pontos e subespaço.

Na figura acima, o ponto no topo está apontando para um ponto no espaço. Neste desenho em particular, o espaço é bidimensional, mas devemos pensar de forma abstrata. O espaço é representado pelo plano cartesiano e a linha em que a pequena pessoa se encontra é um subespaço de pontos. A projecção para este subespaço é o lugar que está mais próximo do ponto original. A geometria diz-nos que podemos encontrar este ponto mais próximo deixando cair uma linha perpendicular (linha pontilhada) do ponto para o espaço. A pequena pessoa está de pé sobre a projecção. A quantidade que essa pessoa teve que caminhar desde a origem até o novo ponto projetado é chamada de coordenada.
Para a explicação das projeções, vamos usar a notação padrão da matriz álgebra para pontos: é um ponto no espaço -dimensional e é menor subespaço.
Exemplo simples com N=2
Se deixarmos . Podemos plotá-lo assim:
mypar (1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)text(2,3," Y",pos=4,cex=3)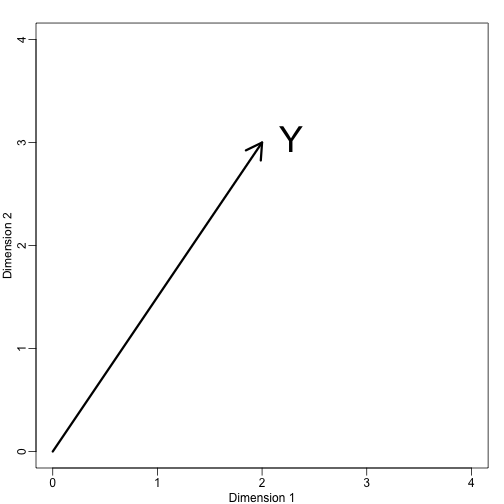
Podemos definir imediatamente um sistema de coordenadas projetando este vetor para o espaço definido por: (o eixo x) e (o eixo y). As projecções do subespaço definidas por estes pontos são 2 e 3 respectivamente:
Dizemos que e são as coordenadas e que são as bases.
Agora vamos definir um novo subespaço. A linha vermelha no gráfico abaixo é subespacial definida por pontos que satisfazem com . A projeção de onto é o ponto mais próximo de . Então precisamos encontrar o que minimiza a distância entre e . Em álgebra linear, aprendemos que a diferença entre estes pontos é ortogonal ao espaço assim:
isto implica que:
e:
Aqui o ponto representa o produto do ponto: .
O seguinte código R confirma que esta equação funciona:
mypar(1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)abline(0,0.5,col="red",lwd=3) #if x=2c and y=c then slope is 0.5 (y=0.5x)text(2,3," Y",pos=4,cex=3)y=c(2,3)x=c(2,1)cc = crossprod(x,y)/crossprod(x)segments(x*cc,x*cc,y,y,lty=2)text(x*cc,x*cc,expression(hat(Y)),pos=4,cex=3)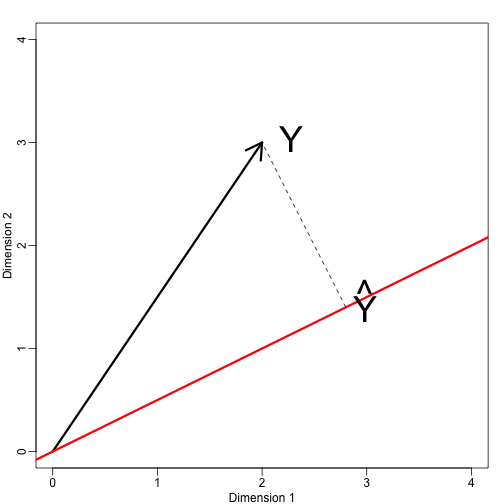
Nota que se era tal, então é simplesmente e o espaço não muda. Esta simplificação é uma das razões porque gostamos de matrizes ortogonais.
Exemplo: A média amostral é uma projecção
Let e é o espaço percorrido por:
Neste espaço, todos os componentes dos vectores são o mesmo número, por isso podemos pensar neste espaço como representando as constantes: na projecção cada dimensão será o mesmo valor. Então o que minimiza a distância entre ?
Quando falamos de problemas como este, às vezes usamos figuras bidimensionais como a que está acima. Simplesmente abstraímos e pensamos como um ponto dentro e como um subespaço definido por um número menor de valores, neste caso apenas um: .
Voltando à nossa questão, sabemos que a projecção é:
que neste caso é a média:
Aqui, também teria sido tão fácil de usar cálculo:
Exemplo: A regressão também é uma projecção
Deixe-nos dar um exemplo um pouco mais complicado. Regressão linear simples também pode ser explicada com projecções. Nossos dados (não vamos mais usar a notação) é novamente um vetor e nosso modelo prevê com uma linha . We want to find the and that minimize the distance between and the space defined by:
with:
Our matrix is and any point in can be written as .
The equation for the multidimensional version of orthogonal projection is:
which we have seen before and gives us:
And the projection to is therefore: