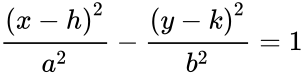Semi-eixo maior | Space Wiki | Organic Articles

Arquivo:Semi-eixo maior.png

O eixo semi-maior de uma elipse

p>Em geometria, o termo eixo semi-maior (também eixo semimajor) é usado para descrever as dimensões de elipses e hipérboles.

Ellipse
Hyperbola
Astronomy
Orbital period
Distância média
Energia; cálculo do eixo semi-maior a partir de vectores de estado
Exemplo

Ellipse

O eixo maior de uma elipse é o seu maior diâmetro, uma linha que percorre o centro e ambos os focos, estando as suas extremidades nos pontos mais largos da forma. O eixo semi-maior é uma metade do eixo maior, e assim corre do centro, através de um foco, até a borda da elipse.

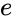
Está relacionado com o eixo semi-maior ${\i1}displaystyle b\,\i$ através da excentricidade ${\i1}displaystyle e\i,{\i}!$ e o semi-latus rectum ${{\an8}displaystyle<img src=$ {\i1}displaystyle b=a{\i1-e^{2}},{\i}!!{\i}” class=”alignleft”> $\ell =a(1-e^{2})\,\!$ {\i1}displaystyle b=a(1-e^{2});{\i}. ${\i1}displaystyle a}ell =b^{2},{\i}$ .

Uma parábola pode ser obtida como o limite de uma sequência de elipses onde um foco é mantido fixo como o outro é permitido mover arbitrariamente para longe numa direcção, mantendo ${\an828154d44$ {\an828154d}{\an8}{\an828154d} >displaystyle {\an8}ell,{\an8}” class=”alignright”> fixed. Assim ${\i1}displaystyle a=,{\i}$ e ${\i1}displaystyle b=,{\i}!}$ tendem ao infinito, ${\i1}displaystyle a=,{\i}!Div> mais rápido que$ {\i1}{\i1}displaystyle b\,\i>,\i>/div>.

p> O eixo semi-maior é o valor médio das menores e maiores distâncias de um foco até aos pontos da elipse. Agora considere a equação em coordenadas polares, com um foco na origem e o outro no eixo positivo x, ${\i1}{\i1-e\i1}displaystyle r(1-e\i}theta )=l,{\i}!}$

The mean value of $r={\ell \over {1+e}}\,\!$ and $r={\ell \over {1-e}}\,\!$ , is $a={\ell \over {1-e^{2}}}\,\!$ .

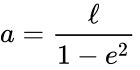
Hyperbola

The semi-major axis of a hyperbola is one half of the distance between the two branches; if this is a in the x-direction the equation is:

${\frac {\left(x-h\right)^{2}}{a^{2}}}-{\frac {\left(y-k\right)^{2}}{b^{2}}}=1$

In terms of the semi-latus rectum and the eccentricity we have

$a={\ell \over e^{2}-1}$

Astronomy

Orbital period

In astrodynamics the orbital period 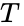$T\,$ of a small body orbiting a central body in a circular or elliptical orbit is:

$T=2\pi {\sqrt {a^{3}/\mu }}$

where:

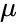
${\i1}$ é o comprimento do eixo semi-máximo da órbita ${\i1}{\i1}displaystyle \u }$ é o parâmetro gravitacional padrão

Notem que para todas as elipses com um determinado eixo semi-máximo, o período orbital é o mesmo, independentemente da excentricidade.

Em astronomia, o eixo semi-maior é um dos elementos orbitais mais importantes de uma órbita, juntamente com o seu período orbital. Para objetos do sistema solar, o eixo semi-maior está relacionado ao período da órbita pela terceira lei de Kepler (originalmente derivada empiricamente),

$T^{2}=a^{3}\,$

onde T é o período em anos, e a é o eixo semi-maior em unidades astronômicas. Esta forma acaba por ser uma simplificação da forma geral para o problema de dois corpos, como determinado por Newton:

${\\displaystyle T^{2}={\frac {4\pi ^{2}}{G(M+m)}}a^{3,}$

onde G é a constante gravitacional, e M é a massa do corpo central, e m é a massa do corpo em órbita. Tipicamente, a massa do corpo central é muito maior que a do corpo em órbita, que m pode ser ignorada. Fazendo essa suposição e usando unidades típicas de astronomia resulta na forma mais simples que Kepler descobriu.

Completamente, o caminho do corpo em órbita ao redor do baricentro e seu caminho em relação ao seu principal são ambos elipses. O eixo semi-maior utilizado em astronomia é sempre a distância entre o primário e o secundário; assim, os parâmetros orbitais dos planetas são dados em termos heliocêntricos. A diferença entre as órbitas primocêntrica e “absoluta” pode ser melhor ilustrada olhando para o sistema Terra-Lua. A relação de massa neste caso é 81.30059. A distância característica Terra-Lua, o eixo semi-maior da órbita lunar geocêntrica, é de 384.400 km. A órbita lunar baricêntrica, por outro lado, tem um eixo semi-maior de 379.700 km, o contra-orbit da Terra ocupando a diferença, 4.700 km. A velocidade média da órbita baricêntrica da Lua é de 1,010 km/s, enquanto a da Terra é de 0,012 km/s. O total destas velocidades dá à velocidade orbital média lunar geocêntrica, 1,022 km/s; o mesmo valor pode ser obtido considerando apenas o valor do eixo semi-maior geocêntrico.

Distância média

Diz-se frequentemente que o eixo semi-maior é a distância “média” entre o primário (o foco da elipse) e o corpo orbital. Isto não é muito preciso, pois depende do que a média é tomada.

média da distância sobre a anomalia excêntrica (q.v.) de fato resulta no eixo semi-maior.
média sobre a anomalia verdadeira (o ângulo orbital verdadeiro, medido no foco) resulta, curiosamente, no eixo semi-menor ${\i1-e^{\i}},{\i},{\i},>{\i}}$ .
média da anomalia média (a fração do período orbital que passou desde o pericentro, expressa como um ângulo), finalmente, dá a média de tempo (que é o que “média” geralmente significa para o leigo): ${\i1+{\i1}{e^{\i}{2}){\i1},{\i}$ .

A média do tempo do inverso do raio, ${\an8}{\an8}displaystyle r^{-1},{\an8}$ ${\an8}displaystyle a^{-1},{\an8}$ .

Energia; cálculo do eixo semi-maior a partir de vectores de estado

Em astrodinâmica eixo semi-maior ${\i1}{\i1}displaystyle a\,}$ pode ser calculado a partir de vectores de estado orbital:

$a={-\mu \over {2\epsilon }}\,$ for an elliptical orbit and $a={\mu \over {2\epsilon }}\,$ for a hyperbolic trajectory

and

$\epsilon ={v^{2} \over {2}}-{\mu \over \left|\mathbf {r} \right|}$ (specific orbital energy)

and

$\mu =GM\,$ (standard gravitational parameter),

where:

$v\,$ is orbital velocity from velocity vector of an orbiting object,
$\mathbf {r} \,$ is cartesian position vector of an orbiting object in coordinates of a reference frame with respect to which the elements of the orbit are to be calculated (e.g. equatorial geocêntrico para uma órbita ao redor da Terra, ou eclíptico heliocêntrico para uma órbita ao redor do Sol),
$G\,$ é a constante gravitacional,
$M\,$ é a massa do corpo central.

Nota que para um dado corpo central e energia específica total, o eixo semi-maior é sempre o mesmo, independentemente da excentricidade. Em contrapartida, para um dado corpo central e eixo semi-maior, a energia específica total é sempre a mesma.

Exemplo

A Estação Espacial Internacional tem um período orbital de 91,74 minutos, daí que o eixo semi-maior seja de 6738 km. Cada minuto a mais corresponde a cerca de 50 km a mais: os 300 km adicionais de comprimento de órbita levam 40 segundos, a velocidade mais baixa contabiliza mais 20 segundos.