MO-Theorie und konjugierte Pi-Bindungen
Der Vorteil der Verwendung der MO-Theorie zum Verständnis von Bindungen in organischen Molekülen wird deutlicher, wenn wir über pi-Bindungen nachdenken. Betrachten wir zunächst die pi-Bindung in Ethen aus dem Blickwinkel der MO-Theorie (in diesem Beispiel lassen wir die s-Bindungen im Molekül außer Acht und betrachten nur die π-Bindung). Wir beginnen mit zwei Atomorbitalen: ein unhybridisiertes 2p-Orbital von jedem Kohlenstoff. Jedes enthält ein einzelnes Elektron. In der MO-Theorie verbinden sich die beiden Atomorbitale mathematisch zu zwei pi-Molekülorbitalen, einem energiearmen pi-Bindungsorbital und einem energiereichen pi*-Antibindungsorbital.
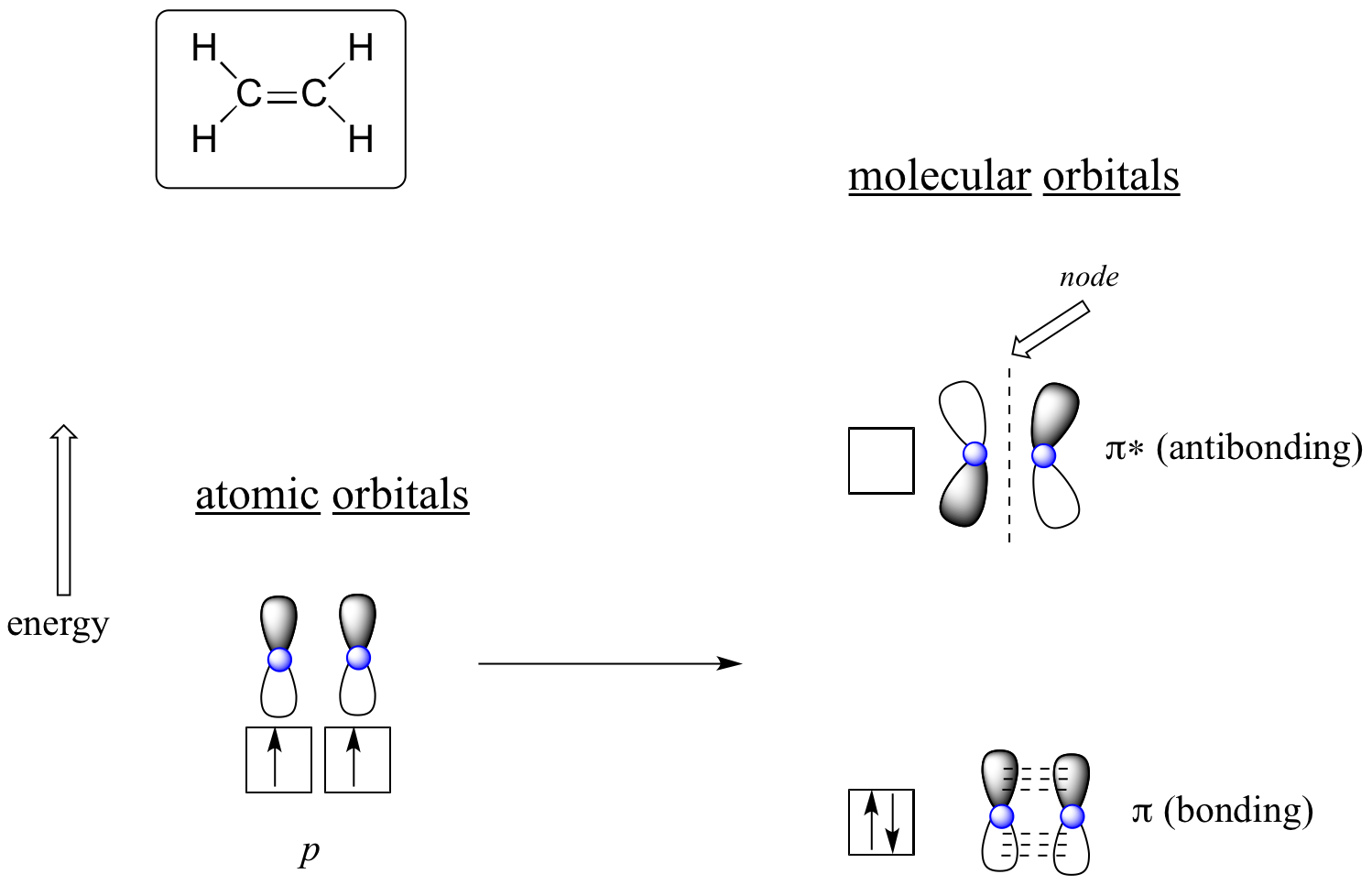
Molekulare Orbitale für Ethen (Ethylen)
Im bindenden p-Orbital wechselwirken die beiden schattierten Lappen der p-Orbitale konstruktiv miteinander, ebenso wie die beiden nicht schattierten Lappen (zur Erinnerung: die willkürliche Wahl der Schattierung stellt mathematische (+) und (-) Zeichen für die mathematische Wellenfunktion dar, die das Orbital beschreibt). Es besteht eine erhöhte Elektronendichte zwischen den beiden Kohlenstoffkernen im Molekülorbital – es handelt sich um eine bindende Wechselwirkung.
Im energiereichen antibindenden pi*-Orbital tritt der schattierte Lappen des einen p-Orbitals in destruktive Wechselwirkung mit dem nicht schattierten Lappen des zweiten p-Orbitals, was zu einem Knoten zwischen den beiden Kernen und zu einer allgemeinen Abstoßung zwischen den Kohlenstoffkernen führt.
Wiederum nach dem Aufbauprinzip platzieren wir die beiden Elektronen in das energieärmere, bindende pi-Molekülorbital. Das antibindende pi*-Orbital bleibt leer.
Als Nächstes betrachten wir das 1,3-Butadien-Molekül. Allein aufgrund der Valenzorbitaltheorie könnte man erwarten, dass die C2-C3-Bindung in diesem Molekül, da es sich um eine Sigma-Bindung handelt, frei rotieren kann.

Experimentell wird jedoch beobachtet, dass es eine erhebliche Barriere für die Rotation um die C2-C3-Bindung gibt und dass das gesamte Molekül planar ist. Außerdem ist die C2-C3-Bindung 148 pm lang und damit kürzer als eine typische Kohlenstoff-Kohlenstoff-Einfachbindung (ca. 154 pm), aber länger als eine typische Doppelbindung (ca. 134 pm).
Die Molekülorbitaltheorie erklärt diese Beobachtungen mit dem Konzept der delokalisierten pi-Bindungen. In diesem Bild verbinden sich die vier 2p-Atomorbitale mathematisch zu vier pi-Molekülorbitalen mit steigender Energie. Zwei davon – die bindenden pi-Orbitale – haben eine niedrigere Energie als die p-Atomorbitale, aus denen sie gebildet werden, während zwei – die antibindenden pi*-Orbitale – eine höhere Energie haben.

Das Molekülorbital mit der niedrigsten Energie, pi1, hat nur eine konstruktive Wechselwirkung und keine Knoten. Das Orbital pi2 ist energetisch höher, aber immer noch niedriger als die isolierten p-Orbitale und hat einen Knoten, aber zwei konstruktive Wechselwirkungen – es ist also insgesamt immer noch ein Bindungsorbital. Betrachtet man die beiden antibindenden Orbitale, so hat pi3* zwei Knoten und eine konstruktive Wechselwirkung, während pi4* drei Knoten und null konstruktive Wechselwirkungen aufweist.
Nach dem Aufbauprinzip werden die vier Elektronen aus den isolierten 2pz-Atomorbitalen in den bindenden pi1- und pi2-MOs platziert. Da pi1 eine konstruktive Wechselwirkung zwischen C2 und C3 einschließt, besteht im 1,3-Butadienmolekül eine gewisse pi-bindende Wechselwirkung zwischen diesen beiden Kohlenstoffen, die für seine kürzere Länge und die Rotationsbarriere verantwortlich ist. Das Valenzbindungsbild von 1,3-Butadien zeigt, dass die beiden pi-Bindungen voneinander isoliert sind, wobei jedes Paar von pi-Elektronen in seiner eigenen pi-Bindung „steckt“. Die Molekülorbitaltheorie sagt jedoch (genau) voraus, dass die vier pi-Elektronen bis zu einem gewissen Grad delokalisiert oder über das gesamte pi-System „verteilt“ sind.
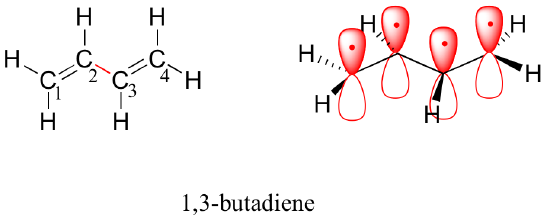
Raumfüllende Ansicht
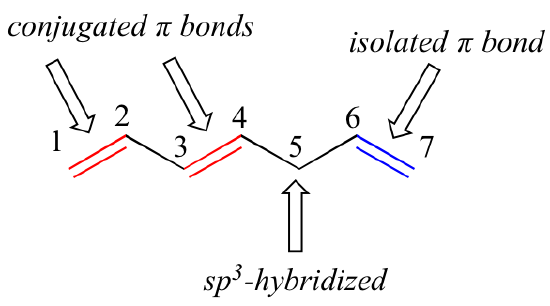
1,3-Butadien ist das einfachste Beispiel für ein System konjugierter pi-Bindungen. Um als konjugiert zu gelten, müssen zwei oder mehr pi-Bindungen durch nur eine Einfachbindung voneinander getrennt sein – mit anderen Worten, es darf kein sp3-hybridisiertes Kohlenstoffatom dazwischen liegen, da dies das überlappende System paralleler p-Orbitale aufbrechen würde. In der nachstehenden Verbindung sind beispielsweise die C1-C2- und C3-C4-Doppelbindungen konjugiert, während die C6-C7-Doppelbindung durch das sp3-hybridisierte C5 von den beiden anderen pi-Bindungen isoliert ist.
Ein sehr wichtiges Konzept, das man im Auge behalten sollte, ist die Tatsache, dass mit der Konjugation eine inhärente thermodynamische Stabilität verbunden ist. Diese Stabilität kann experimentell gemessen werden, indem man die Hydrierungswärme von zwei verschiedenen Dienen vergleicht. (Bei der Hydrierung handelt es sich um einen Reaktionstyp, über den wir in Kapitel 15 mehr erfahren werden: Im Wesentlichen handelt es sich um den Prozess der Anlagerung eines Wasserstoffmoleküls – zwei Protonen und zwei Elektronen – an eine p-Bindung). Wenn die beiden konjugierten Doppelbindungen von 1,3-Pentadien „hydriert“ werden, um Pentan zu erzeugen, werden etwa 225 kJ pro Mol gebildetes Pentan freigesetzt. Zum Vergleich: Bei der Hydrierung der beiden isolierten Doppelbindungen in 1,4-Pentadien, bei der ebenfalls Pentan entsteht, werden etwa 250 kJ/Mol freigesetzt.
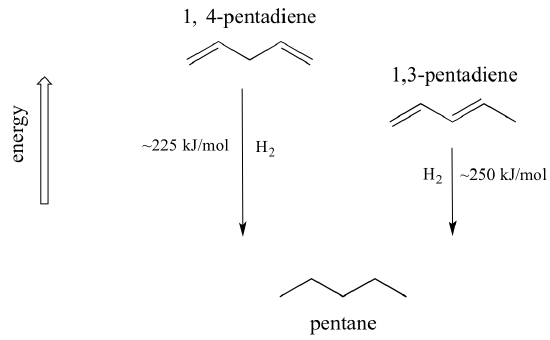
Das konjugierte Dien hat eine niedrigere Energie, ist also stabiler. Im Allgemeinen sind konjugierte pi-Bindungen stabiler als isolierte pi-Bindungen.
Konjugierte pi-Systeme können neben Kohlenstoff auch Sauerstoff- und Stickstoffatome enthalten. Im Stoffwechsel von Fettmolekülen sind einige der wichtigsten Reaktionen mit Alkenen verbunden, die mit Carbonylgruppen konjugiert sind.

In Kapitel 4 werden wir sehen, dass die MO-Theorie sehr nützlich ist, um zu erklären, warum organische Moleküle, die ausgedehnte Systeme konjugierter pi-Bindungen enthalten, oft charakteristische Farben haben. Beta-Carotin, die Verbindung, die für die orange Farbe von Karotten verantwortlich ist, hat ein ausgedehntes System von 11 konjugierten pi-Bindungen.
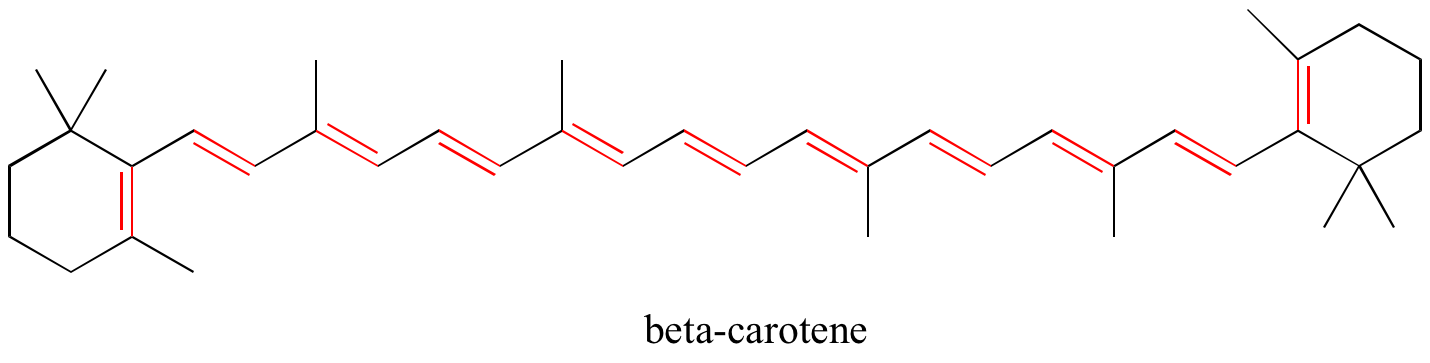
Übung: Identifizieren Sie alle konjugierten und isolierten Doppelbindungen in den untenstehenden Strukturen. Geben Sie für jedes konjugierte pi-System die Anzahl der überlappenden p-Orbitale an und wie viele pi-Elektronen unter ihnen geteilt werden.
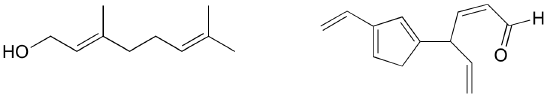
Übung: Bestimmen Sie alle isolierten und konjugierten pi-Bindungen in Lycopin, der rot gefärbten Verbindung in Tomaten. Wie viele pi-Elektronen sind in dem konjugierten pi-System enthalten?

Lösungen zu den Aufgaben
Aromatizität – Das ultimative konjugierte System
Die Molekülorbitaltheorie ist besonders hilfreich, um die einzigartigen Eigenschaften von aromatischen Verbindungen wie Benzol zu erklären:
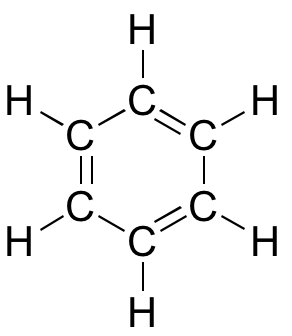
Interaktives 3D-Modell von Benzol
Obwohl Benzol meist mit drei Doppelbindungen und drei Einfachbindungen gezeichnet wird, sind in Wirklichkeit alle Kohlenstoff-Kohlenstoff-Bindungen genau gleich lang (138 pm). Darüber hinaus sind die pi-Bindungen in Benzol deutlich weniger reaktiv als „normale“ pi-Bindungen, entweder isoliert oder konjugiert. Irgendetwas an der Struktur von Benzol macht seine pi-Bindungsanordnung besonders stabil. Dieses „Etwas“ hat einen Namen: Es wird „Aromatizität“ genannt.
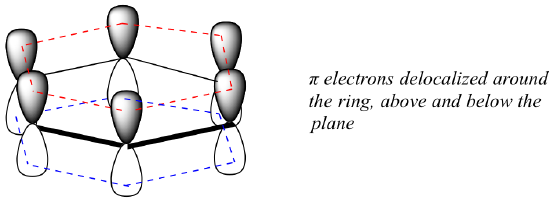
Was genau ist diese „aromatische“ Eigenschaft, die die pi-Bindungen in Benzol so stabil macht? Die Antwort auf diese Frage liegt zum großen Teil in der Tatsache, dass Benzol ein zyklisches Molekül ist, in dem alle Ringatome sp2-hybridisiert sind. Dadurch können die pi-Elektronen in Molekülorbitalen delokalisiert werden, die sich rund um den Ring, über und unter der Ebene erstrecken. Damit dies geschehen kann, muss der Ring natürlich planar sein – sonst könnten sich die p-Orbitale nicht richtig überlappen. Benzol ist bekanntlich ein flaches Molekül.
Sind alle zyklischen Moleküle mit abwechselnden Einfach- und Doppelbindungen ebenso aromatisch stabil? Die Antwort lautet: Nein. Der unten gezeigte achtgliedrige Cyclooctatetraenring ist nicht flach, und seine π-Bindungen reagieren wie „normale“ Alkene.
Es braucht eindeutig mehr, um aromatisch zu sein, und das lässt sich am besten mit der Molekülorbitaltheorie erklären. Sehen wir uns ein Energiediagramm der pi-Molekülorbitale in Benzol an.
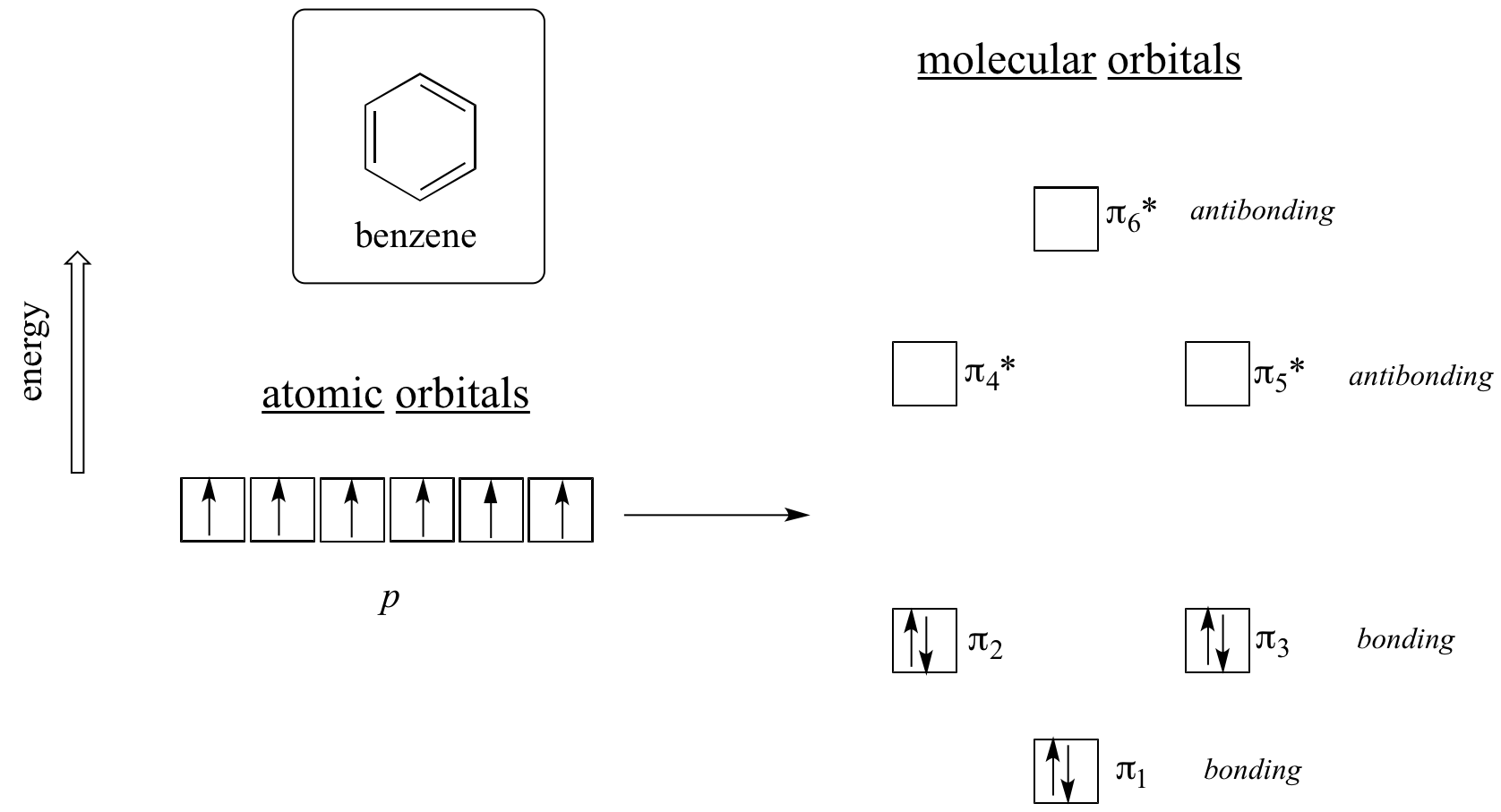
Quantenmechanische Berechnungen zeigen, dass die sechs pi-Molekülorbitale in Benzol, die aus sechs atomaren p-Orbitalen gebildet werden, vier verschiedene Energieniveaus einnehmen. pi1 und pi6* haben eindeutige Energieniveaus, während die Paare pi2 – pi3 und pi4* – pi5* entartet sind, d. h. sie befinden sich auf demselben Energieniveau. Wenn wir das Aufbauprinzip anwenden, um diese Orbitale mit den sechs pi-Elektronen in Benzol aufzufüllen, sehen wir, dass die Bindungsorbitale vollständig gefüllt sind und die antibindenden Orbitale leer sind. Dies gibt uns einen guten Hinweis auf die Quelle der besonderen Stabilität von Benzol: Ein voller Satz von Bindungs-MOs ähnelt in vielerlei Hinsicht der „vollen Schale“ von Elektronen in den Atomorbitalen der stabilen Edelgase Helium, Neon und Argon.
Lassen Sie uns nun dasselbe für Cyclooctatetraen tun, von dem wir bereits gelernt haben, dass es nicht aromatisch ist.
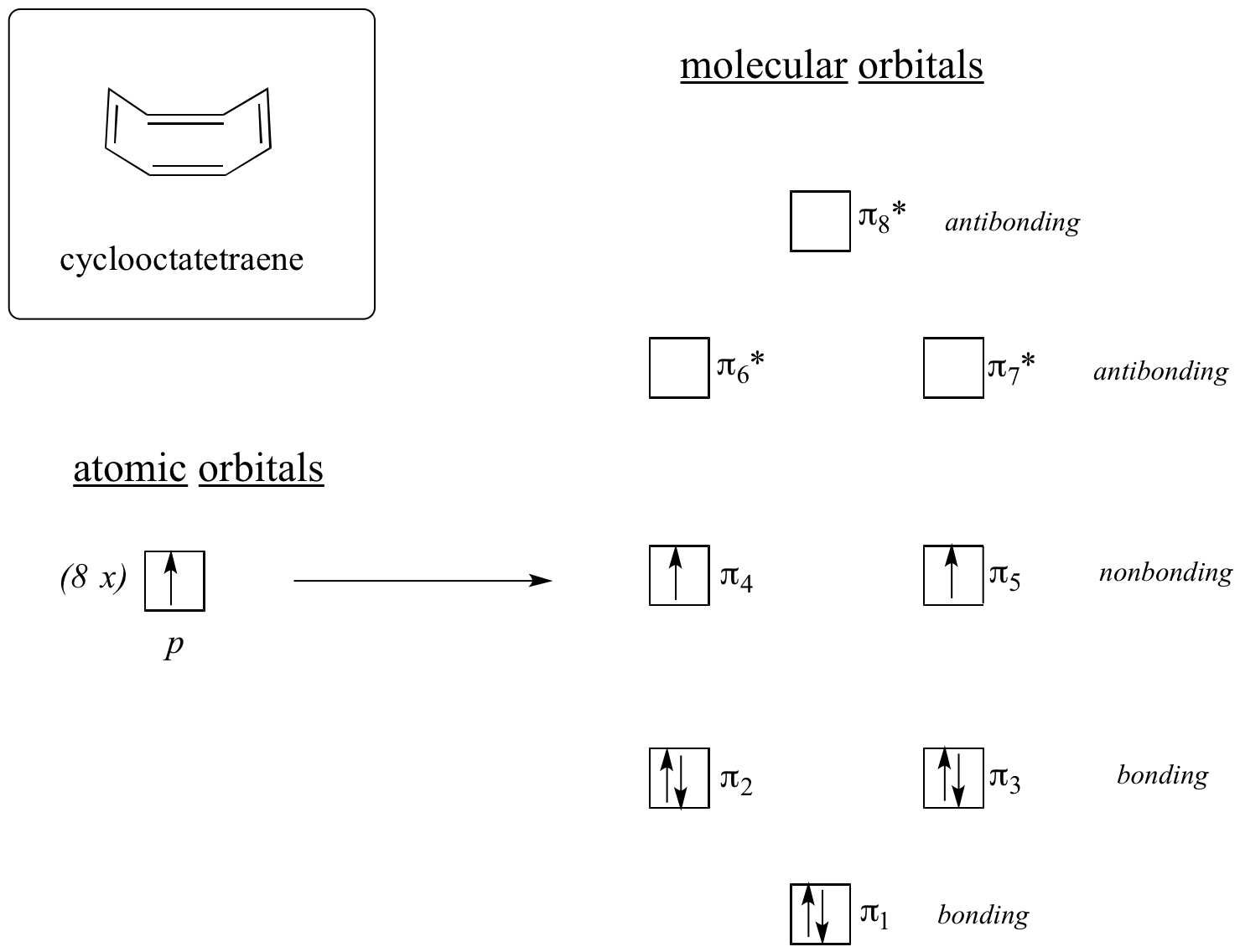
Das Ergebnis der Molekülorbitalberechnungen zeigt uns, dass die niedrigsten und höchsten Energie-MOs (pi1 und pi8*) eindeutige Energieniveaus haben, während die anderen sechs entartete Paare bilden. Beachten Sie, dass pi4 und pi5 auf demselben Energieniveau liegen wie die isolierten 2pz-Atomorbitale: Sie sind also weder bindend noch antibindend, sondern werden als nichtbindende MOs bezeichnet. Füllt man die MOs mit den acht pi-Elektronen des Moleküls auf, so stellt man fest, dass die letzten beiden Elektronen ungepaart sind und in die beiden entarteten nichtbindenden Orbitale fallen. Da wir keine perfekt gefüllte Schale mit bindenden MOs haben, ist unser Molekül nicht aromatisch. Infolgedessen verhält sich jede der Doppelbindungen in Cyclooctatetraen eher wie eine isolierte Doppelbindung.
Das wichtigste Lernziel besteht nun darin, konjugierte pi-Bindungssysteme zu erkennen und zu verstehen, dass Benzol außergewöhnlich stabil ist und eine Eigenschaft aufweist, die man Aromatizität nennt. Die Aromatizität und die Chemie der aromatischen Verbindungen ist relativ komplex und wird in den folgenden Kapiteln dieses Textes ausführlicher behandelt.
Organische Chemie mit biologischem Schwerpunkt von Tim Soderberg (University of Minnesota, Morris)