In unserer Diskussion über das Konfidenzintervall für \(\mu_{Y}\) haben wir die Formel verwendet, um zu untersuchen, welche Faktoren die Breite des Konfidenzintervalls beeinflussen. Das brauchen wir nicht noch einmal zu tun. Da die Formeln so ähnlich sind, stellt sich heraus, dass die Faktoren, die die Breite des Vorhersageintervalls beeinflussen, identisch mit den Faktoren sind, die die Breite des Konfidenzintervalls beeinflussen.
Untersuchen wir stattdessen die Formel für das Vorhersageintervall für \(y_{new}\):
(\hat{y}_h \pm t_{(1-\alpha/2, n-2)} \times \sqrt{MSE \times \left( 1+\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\rechts)}\)
Um zu sehen, wie es im Vergleich zur Formel für das Konfidenzintervall für \(\mu_{Y}\):
(\hat{y}_h \pm t_{(1-\alpha/2, n-2)} \times \sqrt{MSE \left(\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\rechts)}\)
Beachten Sie, dass der einzige Unterschied in den Formeln darin besteht, dass der Standardfehler der Vorhersage für \(y_{new}\) einen zusätzlichen MSE-Term enthält, der Standardfehler der Anpassung für \(\mu_{Y}\) jedoch nicht.
Lassen Sie uns versuchen, das Vorhersageintervall zu verstehen, um zu sehen, was den zusätzlichen MSE-Term verursacht. Beginnen wir dabei zunächst mit einem einfacheren Problem. Überlegen Sie, wie wir eine neue Antwort \(y_{new}\) an einem bestimmten \(x_{h}\) vorhersagen könnten, wenn der Mittelwert der Antworten \(\mu_{Y}\) an \(x_{h}\) bekannt wäre. Das heißt, angenommen, es wäre bekannt, dass die mittlere Hautkrebssterblichkeit bei \(x_{h} = 40^{o}\) N 150 Todesfälle pro Million (mit einer Varianz von 400) beträgt? Wie hoch ist die vorhergesagte Hautkrebssterblichkeit in Columbus, Ohio?
Da \(\mu_{Y} = 150 \) und \( \sigma^{2} = 400\) bekannt sind, können wir die „empirische Regel“ nutzen, die unter anderem besagt, dass 95 % der Messwerte normalverteilter Daten innerhalb von 2 Standardabweichungen vom Mittelwert liegen. Das heißt, sie besagt, dass 95% der Messungen in dem Intervall liegen, das zwischen:
(\mu_{Y}- 2\sigma\) und \(\mu_{Y}+ 2\sigma\) liegt.
Anwendung der 95%-Regel auf unser Beispiel mit \(\mu_{Y} = 150\) und \(\sigma= 20\):
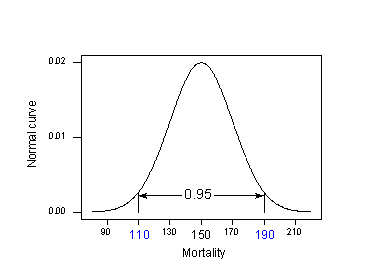
95% der Hautkrebsmortalitätsraten von Orten am 40. nördlichen Breitengrad liegen in dem Intervall zwischen:
150 – 2(20) = 110 und 150 + 2(20) = 190.
Das heißt, wenn jemand die Hautkrebs-Sterblichkeitsrate für einen Ort auf 40 Grad nördlicher Breite wissen wollte, würde unsere beste Schätzung irgendwo zwischen 110 und 190 Todesfällen pro 10 Millionen liegen. Das Problem ist, dass wir bei unserer Berechnung \(\mu_{Y}\) und \(\sigma\) verwendet haben, Bevölkerungswerte, die wir normalerweise nicht kennen würden. Die Realität sieht so aus:
- Der Mittelwert \(\mu_{Y}\) ist in der Regel nicht bekannt. Es ist logisch, ihn mit der vorhergesagten Antwort \(\hat{y}\) zu schätzen. Die Kosten der Verwendung von \(\hat{y}\) zur Schätzung von \(\mu_{Y}\) sind die Varianz von \(\hat{y}\). Das heißt, unterschiedliche Stichproben würden unterschiedliche Vorhersagen \(\hat{y}\) ergeben, und daher müssen wir diese Varianz von \(\hat{y}\) berücksichtigen.
- Die Varianz \( \sigma^{2}\) ist normalerweise nicht bekannt. Es ist logisch, sie mit MSE zu schätzen.
Da wir diese unbekannten Größen schätzen müssen, hängt die Variation in der Vorhersage einer neuen Antwort von zwei Komponenten ab:
- die Variation aufgrund der Schätzung des Mittelwerts \(\mu_{Y}\) mit \(\hat{y}_h\) , die wir als „\(\sigma^2(\hat{Y}_h)\) bezeichnen.(Beachten Sie, dass die Schätzung dieser Größe nur das Quadrat des Standardfehlers der Anpassung ist, das in der Konfidenzintervallformel erscheint.)
- die Variation in den Antworten y, die wir als „\(\sigma^2\)“ bezeichnen.“(Beachten Sie, dass diese Größe wie üblich mit dem mittleren quadratischen Fehler MSE geschätzt wird.)
Addiert man die beiden Varianzkomponenten, erhält man:
(\sigma^2+\sigma^2(\hat{Y}_h)\)
Dies wird geschätzt durch:
(MSE+MSE \left( \dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \right) =MSE\left( 1+\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \right) \)
Kennen Sie diese Größe? Es ist einfach die Varianz der Vorhersage, die in der Formel für das Vorhersageintervall \(y_{new}\) auftaucht!
Lassen Sie uns die beiden Intervalle noch einmal vergleichen:
Konfidenzintervall für \(\mu_{Y}\colon \hat{y}_h \pm t_{(1-\alpha/2, n-2)} \times \sqrt{MSE \times \left( \frac{1}{n} + \frac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\)
Vorhersageintervall für \(y_{new}\colon \hat{y}_h \pm t_{(1-\alpha/2, n-2)} \mal \sqrt{MSE \left( 1+\frac{1}{n} + \frac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\)
Was bedeutet der Unterschied in den beiden Formeln für die Praxis?
- Da das Vorhersageintervall den zusätzlichen MSE-Term enthält, wird ein \( \left( 1-\alpha \right) 100\% \) Konfidenzintervall für \(\mu_{Y}\) bei \(x_{h}\) immer schmaler sein als das entsprechende \( \left( 1-\alpha \right) 100\% \) Vorhersageintervall für \(y_{new}\) bei \(x_{h}\).
- Bei der Berechnung des Intervalls beim Stichprobenmittelwert der Prädiktorenwerte \(\left(x_{h} = \bar{x}\right)\) und der Vergrößerung des Stichprobenumfangs n kann sich der Standardfehler des Konfidenzintervalls 0 nähern. Da das Vorhersageintervall den zusätzlichen MSE-Term enthält, kann der Standardfehler des Vorhersageintervalls nicht in die Nähe von 0 gelangen.
Die erste Implikation wird am einfachsten deutlich, wenn man das folgende Diagramm für unser Beispiel der Hautkrebsmortalität betrachtet:
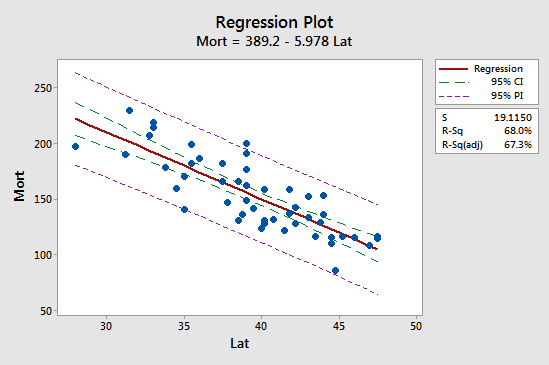
Beobachten Sie, dass das Vorhersageintervall (95% PI, in lila) immer breiter ist als das Konfidenzintervall (95% CI, in grün). Außerdem sind beide Intervalle am engsten beim Mittelwert der Vorhersagewerte (etwa 39,5).