In diesem Abschnitt werden wir lernen, wie man die Wurzel(n) einer quadratischen Gleichung findet. Wurzeln werden auch als x-Schnittpunkte oder Nullstellen bezeichnet. Eine quadratische Funktion wird grafisch durch eine Parabel dargestellt, deren Scheitelpunkt im Ursprung, unterhalb der x-Achse oder oberhalb der x-Achse liegt. Daher kann eine quadratische Funktion eine, zwei oder null Wurzeln haben.
Wenn wir aufgefordert werden, eine quadratische Gleichung zu lösen, geht es eigentlich darum, die Wurzeln zu finden. Wir haben bereits gesehen, dass die Vervollständigung des Quadrats eine nützliche Methode zur Lösung quadratischer Gleichungen ist. Mit dieser Methode lässt sich die quadratische Formel ableiten, die zur Lösung quadratischer Gleichungen verwendet wird. Die Wurzeln der Funktion
f (x) = ax2 + bx + c
sind nämlich durch die quadratische Formel gegeben. Die Wurzeln einer Funktion sind die x-Achsenabschnitte. Per Definition ist die y-Koordinate von Punkten, die auf der x-Achse liegen, Null. Um die Wurzeln einer quadratischen Funktion zu finden, setzt man also f (x) = 0 und löst die Gleichung
ax2 + bx + c = 0.
We can do this by completing the square as,
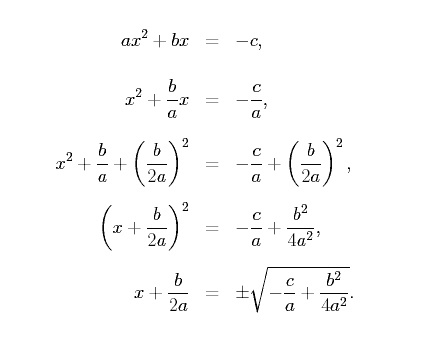
Solving for x and simplifying we have,
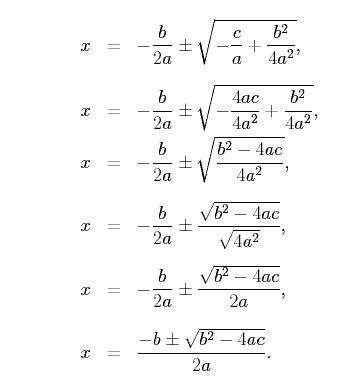
Thus, the roots of a quadratic function are given by,
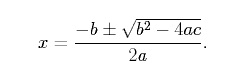
This formula is called the quadratic formula, and its derivation is included so that you can see where it comes from. We call the term b2 −4ac the discriminant. The discriminant is important because it tells you how many roots a quadratic function has. Specifically, if
1. b2 −4ac < 0 There are no real roots.
2. b2 −4ac = 0 There is one real root.
3. b2 −4ac > 0 There are two real roots.
We will examine each case individually.
Fall 1: Keine reellen Wurzeln
Wenn die Diskriminante einer quadratischen Funktion kleiner als Null ist, hat diese Funktion keine reellen Wurzeln, und die von ihr dargestellte Parabel schneidet die x-Achse nicht. Da die quadratische Formel die Quadratwurzel der Diskriminante erfordert, stellt eine negative Diskriminante ein Problem dar, da die Quadratwurzel einer negativen Zahl nicht über die reelle Linie definiert ist. Ein Beispiel für eine quadratische Funktion ohne reelle Wurzeln ist gegeben durch
f(x) = x2 – 3x + 4.
Beachte, dass die Diskriminante von f(x) negativ ist,
b2 -4ac = (-3)2- 4 – 1 – 4 = 9 – 16 = -7.
Diese Funktion wird grafisch durch eine nach oben geöffnete Parabel dargestellt, deren Scheitelpunkt oberhalb der x-Achse liegt. Der Graph kann also nie die x-Achse schneiden und hat keine Wurzel, wie unten gezeigt
Fall 2: Eine reelle Wurzel
Wenn die Diskriminante einer quadratischen Funktion gleich Null ist, hat diese Funktion genau eine reelle Wurzel und schneidet die x-Achse in einem einzigen Punkt. Um dies zu sehen, setzen wir b2 -4ac = 0 in die quadratische Formel ein und erhalten
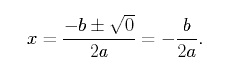
Beachte, dass 
die x-Koordinate des Scheitelpunkts einer Parabel ist. Eine Parabel hat also genau eine reelle Wurzel, wenn der Scheitelpunkt der Parabel genau auf der x-Achse liegt. Das einfachste Beispiel für eine quadratische Funktion mit nur einer reellen Wurzel ist,
y = x2,
wobei die reelle Wurzel x = 0 ist.
Ein weiteres Beispiel für eine quadratische Funktion mit einer reellen Wurzel ist gegeben durch,
f(x) = -4×2 + 12x – 9.
Beachte, dass die Diskriminante von f(x) Null ist,
b2 -4ac = (12)2- 4 – -4 – -9 = 144 – 144 = 0.
Diese Funktion wird grafisch durch eine Parabel dargestellt, die sich nach unten öffnet und deren Scheitelpunkt (3/2, 0) auf der x-Achse liegt. Thus, the graph intersects the x-axis at exactly one point (i.e. has one root) as shown below,
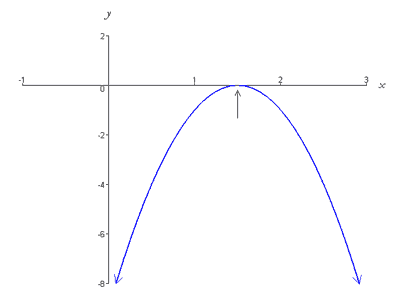
Case 3: Two Real Roots
If the discriminant of a quadratic function is greater than zero, that function has two real roots (x-intercepts). Taking the square root of a positive real number is well defined, and the two roots are given by,
An example of a quadratic function with two real roots is given by,
f(x) = 2×2− 11x + 5.
Notice that the discriminant of f(x) is greater than zero,