In onze bespreking van het betrouwbaarheidsinterval voor (\mu_{Y}) hebben we de formule gebruikt om te onderzoeken welke factoren van invloed zijn op de breedte van het betrouwbaarheidsinterval. Het is niet nodig om dat nog eens te doen. Omdat de formules zo op elkaar lijken, blijkt dat de factoren die van invloed zijn op de breedte van het voorspellingsinterval identiek zijn aan de factoren die van invloed zijn op de breedte van het betrouwbaarheidsinterval.
Laten we in plaats daarvan de formule voor het voorspellingsinterval voor \(y_{new}}) onderzoeken:
(\hat{y}_h \pm t_{(1-)-alpha/2, n-2)} \maal \sqrt{MSE maal \links( 1+dfrac{1}{n}
om te zien hoe dit zich verhoudt tot de formule voor het betrouwbaarheidsinterval voor \(\mu_{Y}):
(\hat{y}_h \pm t_{(1-alfa/2, n-2)} \maal \sqrt{MSE \links(\dfrac{1}{n}
Opgemerkt moet worden dat het enige verschil in de formules is dat de standaardfout van de voorspelling voor \(y_{new}}) een extra MSE-term in zich heeft en de standaardfout van de fit voor \(\mu_{Y}}) niet.
Laten we proberen het voorspellingsinterval te begrijpen om te zien wat de oorzaak is van de extra MSE-term. Laten we daarbij eerst met een eenvoudiger probleem beginnen. Bedenk hoe we een nieuwe respons (y_{new}) op een bepaalde \(x_{h}) zouden kunnen voorspellen als het gemiddelde van de responsen \(\mu_{Y}) op \(x_{h}) bekend zou zijn. Dat wil zeggen, stel dat bekend is dat de gemiddelde sterfte aan huidkanker bij x_{h} = 40^{o}}) N 150 sterfgevallen per miljoen is (met variantie 400)? Wat is dan de voorspelde sterfte aan huidkanker in Columbus, Ohio?
Omdat \(\mu_{Y} = 150 \) en \( \sigma^{2} = 400 \) bekend zijn, kunnen we gebruik maken van de “empirische regel”, die onder andere stelt dat 95% van de metingen van normaal verdeelde gegevens binnen 2 standaarddeviaties van het gemiddelde liggen. Dat wil zeggen dat 95% van de metingen in het interval ligt tussen:
(\mu_{Y}- 2\sigma) en \(\mu_{Y}+ 2\sigma).
Toepassing van de 95% regel op ons voorbeeld met \(\mu_{Y} = 150%) en \(\sigma= 20%):
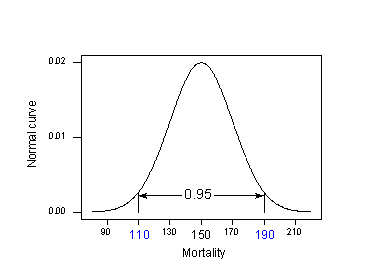
95% van de sterftecijfers voor huidkanker van locaties op 40 graden noorderbreedte liggen in het interval ingeklemd door:
150 – 2(20) = 110 en 150 + 2(20) = 190.
Dat wil zeggen, als iemand het sterftecijfer voor huidkanker zou willen weten voor een plaats op 40 graden noorderbreedte, zou onze beste schatting ergens tussen 110 en 190 sterfgevallen per 10 miljoen liggen. Het probleem is dat onze berekening gebruik maakte van \mu_{Y}} en \sigma}, bevolkingswaarden die we normaal gesproken niet zouden kennen. De realiteit doet zich voor:
- Het gemiddelde \(\mu_{Y}}) is normaal gesproken niet bekend. Het is logisch om het te schatten met de voorspelde respons \(u_{Y}). De kosten van het gebruik van (\hat{y}}) om (\mu_{Y}}) te schatten is de variantie van \(\hat{y}}). Dat wil zeggen, verschillende steekproeven zouden verschillende voorspellingen opleveren, en dus moeten we rekening houden met deze variantie van (\hat{y}}).
- De variantie \( \sigma^{2}\) is meestal niet bekend. Het is logisch om deze met MSE te schatten.
Omdat we deze onbekende grootheden moeten schatten, hangt de variatie in de voorspelling van een nieuwe respons af van twee componenten:
- de variatie als gevolg van het schatten van het gemiddelde (\mu_{Y}) met \hat{y}_h) , die we aanduiden als “\(\sigma^2(\hat{Y}_h)\).”(Merk op dat de schatting van deze grootheid gewoon het kwadraat van de standaardfout van de fit is die in de formule van het betrouwbaarheidsinterval voorkomt.)
- de variatie in de responsen y, die we aanduiden als “\(\sigma^2%).”(Merk op dat deze grootheid, zoals gebruikelijk, wordt geschat met de gemiddelde kwadratische fout MSE.)
Tellen we de twee variantiecomponenten op, dan krijgen we:
(\sigma^2+ \sigma^2(\hat{Y}_h)
die wordt geschat door:
(MSE+MSE \links( \dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \rechts) =MSE-links( 1+{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2}
Herken je deze grootheid? Het is gewoon de variantie van de voorspelling die voorkomt in de formule voor het voorspellingsinterval (y_{new}})!
Laten we de twee intervallen nog eens vergelijken:
Betrouwbaarheidsinterval voor \(\mu_{Y})\kolon \hat{y}_h \pm t_{(1-alpha/2, n-2)} \maal \sqrt{MSE maal \links( \frac{1}{n} + \frac{(x_h-bar{x})^2}{(x_i-bar{x})^2}rechts)})
Voorspellingsinterval voor \(y_{new}]\colon \hat{y}_h \pm t_{(1-alfa/2, n-2)} \maal \sqrt{MSE \left( 1+\frac{1}{n}
Wat zijn de praktische consequenties van het verschil in de twee formules?
- Omdat het voorspellingsinterval de extra MSE-term heeft, zal een \links( 1-alpha \rechts) 100% \) betrouwbaarheidsinterval voor \(\mu_{Y}}) bij \(x_{h}}) altijd smaller zijn dan het overeenkomstige \links( 1-alpha \rechts) 100% \) voorspellingsinterval voor \(y_{new}}) bij \(x_{h}}).
- Door het interval te berekenen bij het steekproefgemiddelde van de voorspellende waarden \(x_{h} = x_{h} = x_{h})) en de steekproefgrootte n te vergroten, kan de standaardfout van het betrouwbaarheidsinterval 0 benaderen. Omdat het voorspellingsinterval de extra MSE-term heeft, kan de standaardfout van het voorspellingsinterval niet in de buurt van 0 komen.
De eerste implicatie is het gemakkelijkst te zien door de volgende plot voor ons voorbeeld van de sterfte aan huidkanker te bestuderen:
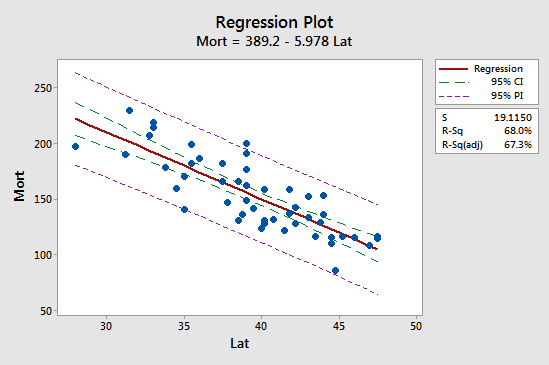
Zie dat het voorspellingsinterval (95% PI, in paars) altijd breder is dan het betrouwbaarheidsinterval (95% CI, in groen). Bovendien zijn beide intervallen het smalst bij het gemiddelde van de voorspellende waarden (ongeveer 39,5).