In dit onderdeel leren we hoe we de wortel(s) van een kwadratische vergelijking kunnen vinden. Wortels worden ook wel x-afsnijdingen of nulpunten genoemd. Een kwadratische functie wordt grafisch voorgesteld door een parabool met het hoekpunt in de oorsprong, onder de x-as, of boven de x-as. Een kwadratische functie kan dus één, twee of nul wortels hebben.
Wanneer ons wordt gevraagd een kwadratische vergelijking op te lossen, wordt ons eigenlijk gevraagd de wortels te vinden. We hebben al gezien dat de kwadratische voltooiing een handige methode is om kwadratische vergelijkingen op te lossen. Deze methode kan worden gebruikt om de kwadratische formule af te leiden, die wordt gebruikt om kwadratische vergelijkingen op te lossen. In feite worden de wortels van de functie
f (x) = ax2 + bx + c
gegeven door de kwadratische formule. De wortels van een functie zijn de x-coördinaten. Per definitie is de y-coördinaat van punten die op de x-as liggen nul. Om de wortels van een kwadratische functie te vinden, stellen we dus f (x) = 0, en lossen we de vergelijking op,
ax2 + bx + c = 0.
We can do this by completing the square as,
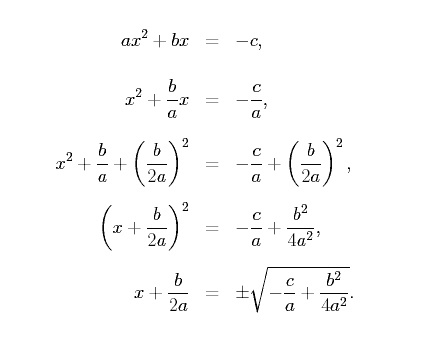
Solving for x and simplifying we have,
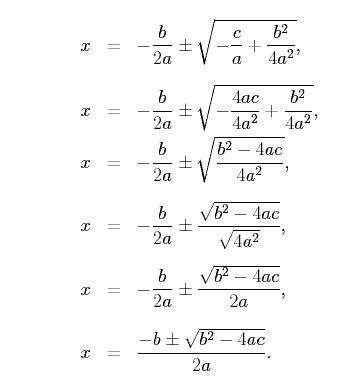
Thus, the roots of a quadratic function are given by,
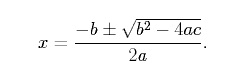
This formula is called the quadratic formula, and its derivation is included so that you can see where it comes from. We call the term b2 −4ac the discriminant. The discriminant is important because it tells you how many roots a quadratic function has. Specifically, if
1. b2 −4ac < 0 There are no real roots.
2. b2 −4ac = 0 There is one real root.
3. b2 −4ac > 0 There are two real roots.
We will examine each case individually.
Geval 1: geen reele wortels
Als de discriminant van een kwadratische functie kleiner is dan nul, heeft die functie geen reele wortels, en snijdt de parabool die hij voorstelt de x-as niet. Aangezien de kwadratische formule vereist dat de vierkantswortel van de discriminant wordt genomen, levert een negatieve discriminant een probleem op omdat de vierkantswortel van een negatief getal niet gedefinieerd is over de reële lijn. Een voorbeeld van een kwadratische functie zonder reele wortels is gegeven door,
f(x) = x2 – 3x + 4.
Merk op dat de discriminant van f(x) negatief is,
b2 -4ac = (-3)2- 4 – 1 – 4 = 9 – 16 = -7.
Deze functie wordt grafisch voorgesteld door een parabool die naar boven toe open gaat en waarvan het hoekpunt boven de x-as ligt. De grafiek kan dus nooit de x-as snijden en heeft geen wortels, zoals hieronder te zien is,
Geval 2: Eén reele wortel
Als de discriminant van een kwadratische functie gelijk is aan nul, dan heeft die functie precies één reele wortel en snijdt hij de x-as in één enkel punt. Om dit te zien stellen we b2 -4ac = 0 in de kwadratische formule om te krijgen,
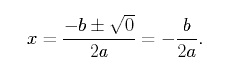
Merk op dat 
de x-coördinaat is van het hoekpunt van een parabool. Een parabool heeft dus precies één reele wortel als het hoekpunt van de parabool precies op de x-as ligt. Het eenvoudigste voorbeeld van een kwadratische functie die slechts één reele wortel heeft is,
y = x2,
waarbij de reele wortel x = 0 is.
Een ander voorbeeld van een kwadratische functie met één reele wortel is gegeven door,
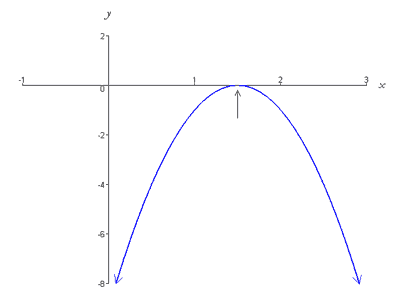
f(x) = -4×2 + 12x – 9.
Merk op dat de discriminant van f(x) nul is,
b2 -4ac = (12)2- 4 – -4 – -9 = 144 – 144 = 0.
Deze functie wordt grafisch voorgesteld door een parabool die naar beneden toe open gaat en het hoekpunt (3/2, 0) heeft, liggend op de x-as. Thus, the graph intersects the x-axis at exactly one point (i.e. has one root) as shown below,
Case 3: Two Real Roots
If the discriminant of a quadratic function is greater than zero, that function has two real roots (x-intercepts). Taking the square root of a positive real number is well defined, and the two roots are given by,
An example of a quadratic function with two real roots is given by,
f(x) = 2×2− 11x + 5.
Notice that the discriminant of f(x) is greater than zero,