Een Cobb-Douglas productiefunctie modelleert de relatie tussen productie-output en productie-inputs (factoren). Zij wordt gebruikt om de verhouding van de inputs tot elkaar te berekenen voor een efficiënte productie en om de technologische veranderingen in de productiemethoden te schatten. De algemene vorm van een Cobb-Douglas productiefunctie voor een reeks van (n) inputs is als volgt: (Y) staat voor de output, (x_{i}) voor de input (i), en (gamma) en (alfa_{i}) zijn parameters die de algemene efficiëntie van de productie en de gevoeligheid van de output voor veranderingen in de inputhoeveelheden bepalen. De toepassing van deze functionele vorm voor het meten van de productie is te danken aan de wiskundige Charles Cobb en de econoom Paul Douglas, die er gebruik van maakten om het relatieve belang van de twee inputfactoren, arbeid en kapitaal, voor de industriële productie in de VS over de periode 1899 tot 1922 te bestuderen. In hun oorspronkelijke model beperken Cobb en Douglas de parameters voor de elasticiteit van de productie tot het bereik \(\alpha_{1}}) en \(\alpha_{2}}) en tot de som van \(\alpha_{i}}in links(0,1}rechts)\) en tot één, hetgeen een constante schaalopbrengst impliceert. De functie is dus \waarbij \(x_{1}) en \(x_{2}) respectievelijk staan voor arbeid en kapitaal. Door de natuurlijke logaritme van beide zijden van de vergelijking te nemen, kunnen voor de gegevens over output, arbeid en kapitaal de parameters \(\gamma) en \(\alpha_{1}) worden geschat met behulp van de gewone kleinste kwadraten. Op basis van hun gegevens komen Cobb en Douglas tot een waarde van 0,75 voor \(\alpha_{1}\), hetgeen betekent dat driekwart van de waarde van de Amerikaanse industriële productie in de onderzochte periode voor rekening van de arbeid komt (het resterende kwart voor rekening van het kapitaal). Hun schatting voor de efficiëntieparameter \(\gamma_{1}) is 1,01, hetgeen, aangezien deze groter is dan 1, de positieve effecten weerspiegelt van niet-waarneembare krachten op de productie via de combinatie van arbeid en kapitaal.
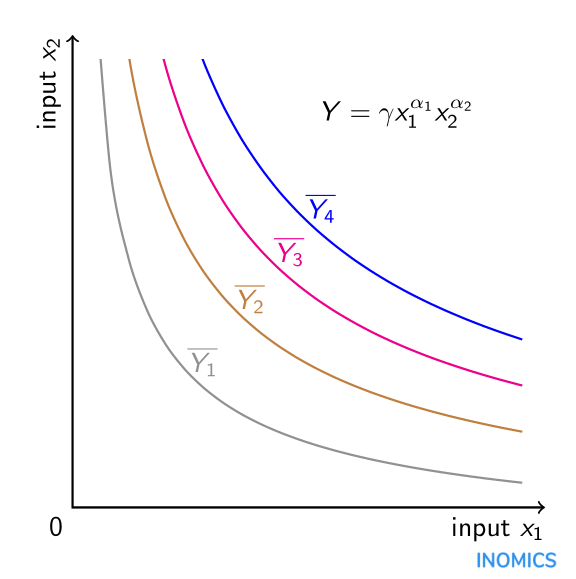
Het multiplicatieve karakter van een Cobb-Douglas productiefunctie, uitgaande van positieve waarden voor \(\alpha_{i}), betekent dat de inputs complementair zijn in de productie. In het standaardmodel van arbeid en kapitaal verhoogt een toename van de hoeveelheid kapitaal de productie niet alleen rechtstreeks, maar ook onrechtstreeks via de invloed ervan op de arbeidsproductiviteit. Mathematisch gezien is de kruispartiële afgeleide van de productie-output \(Y) met betrekking tot arbeid \(x_{1}) en kapitaal \(x_{2}) positief. Bovendien zijn door de aanname dat de afgeleide van de tweede orde van de productie-output ten opzichte van arbeid en ten opzichte van kapitaal beide negatief, wat impliceert dat de marginale opbrengst voor elke input afzonderlijk afneemt. Door eenvoudigweg hetzij meer arbeid, hetzij meer kapitaal (maar niet beide) aan het productieproces toe te voegen, neemt de productie toe, zij het in een afnemend tempo. Bovendien is de elasticiteit van de substitutie tussen de inputs constant en gelijk aan één als gevolg van de functionele vorm. Een Cobb-Douglas-productiefunctie met twee inputs kan grafisch worden voorgesteld in de vorm van isoquanten: combinaties van beide inputs waarvoor de output constant is. Er zijn vier van dergelijke isoquanten in de grafiek hier voor de (constante) outputniveaus \(\overline{Y_{1}}), \(\overline{Y_{2}}), \(\overline{Y_{3}}) en \(\overline{Y_{4}}). Hoe verder de isoquant van de oorsprong, hoe groter het niveau van de output (\overline{Y_{4}}>\overline{Y_{3}}>\overline{Y_{2}}>\overline{Y_{1}}). Welke precieze combinatie van de inputs \(x_{1}} en \(x_{2}}) optimaal is voor de productie wordt bepaald door het budget waarover de producent beschikt en door de kostenverhouding van input \(x_{2}}) ten opzichte van input \(x_{1}}) die in de grafiek kan worden opgenomen in de vorm van een isokostenlijn (zie het artikel over elasticiteit van substitutie).
Cobb en Douglas erkenden zelf dat hun productiefunctie niet op solide theoretische grondslagen berust en ook niet moet worden opgevat als een productiewet; zij vormt slechts een statistische benadering van de waargenomen relaties tussen productie-inputs en output. Niettemin zijn de eenvoudige wiskundige eigenschappen aantrekkelijk voor economen en hebben zij ertoe geleid dat de functie de afgelopen eeuw een standaard is geworden in de micro-economische theorie.
Verder lezen:
Voor de achtergrond en een overzicht van de belangrijkste eigenschappen van Cobb-Douglas-productiefuncties, zie met name de secties 6, 7 en 8 van het oorspronkelijke artikel van Cobb en Douglas, “A Theory of Production” (The American Economic Review, 1928).
Goed om te weten:
De Cobb-Douglas functievorm wordt niet alleen in de productietheorie gebruikt, maar is ook standaard geworden in de micro-economische consumptietheorie, waar zij wordt toegepast als nutsfunctie, waarbij \(Y\) voor het nut \(U\) wordt. De waarden voor \(x_{i}) staan dan voor de consumptie-items en wanneer de nutsfunctie wordt gemaximaliseerd onder een budgetrestrictie, geven de waarden voor \(\alpha_{i}) aan hoe het individu zijn budget optimaal over de items zal verdelen.