
Als je aan spionnen en geheim agenten denkt, denk je misschien aan een heleboel dingen; handige gadgets, buitenlandse reizen, gevaarlijke raketten, snelle auto’s en geschud worden maar niet geroerd. Je zou waarschijnlijk niet aan wiskunde denken. Maar dat zou je wel moeten doen.
Codes kraken en de ware betekenis van geheime boodschappen ontrafelen vergt heel wat wiskunde, van eenvoudig optellen en aftrekken, tot gegevensverwerking en logisch denken. Enkele van de beroemdste codebrekers in de geschiedenis waren wiskundigen die met eenvoudige wiskunde complotten konden ontrafelen, verraders konden identificeren en veldslagen konden beïnvloeden.
De Romeinse Geezer
Laat me je een voorbeeld geven. Bijna 2000 jaar geleden was Julius Caesar bezig de wereld te veroveren, landen binnen te vallen om het Romeinse Rijk te vergroten. Hij had een manier nodig om zijn strijdplannen en tactieken aan iedereen mee te delen zonder dat de vijand erachter kwam. So Caesar would write messages to his generals in code. Instead of writing the letter ‘A’, he would write the letter thatcomes three places further on in the alphabet, the letter ‘D’. Instead of a ‘B’, he would write an ‘E’, instead of a ‘C’, he would write an ‘F’ and so on. When he got to the end of the alphabet, however, he would have to go right back to the beginning, so instead of an ‘X’, he would write an ‘A’, instead of a ‘Y’, he’d write a ‘B’ and instead of ‘Z’, he’d write a ‘C’.
Complete the table to find out how Caesar would encode the following message:
| Caesar’s message | A | T | T | A | C | K | A | T | D | A | W | N | ||
| B | U | |||||||||||||
| C | V | |||||||||||||
| Coded message | D |
When Caesar’s generals came to decipher the messages, they knew that all they had to do was go back three places in the alphabet. Have a go at trying to work out these messages which could have been sent by Caesar or his generals:
hqhpb dssurdfklqj
wkluwb ghdg
uhwuhdw wr iruhvw
Easy as 1, 2, 3
This all seems very clever, but so far it’s all been letters and no numbers. So where’s the maths? The maths comes if you think of the letters as numbers from 0 to 25 with A being 0, B being 1, C being 2 etc. Then encoding, shifting the alphabet forward three places, is the same as adding three to your starting number:
| A | B | C | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
For example, encoding the letter ‘A’ is 0+3=3, which is a ‘D’.
Coding ‘I’ is: 8+3=11, which is ‘L’.
However, you do have to be careful when you get to the end of the alphabet, because there is no letter number 26, so you have to go back to number 0. In maths we call this ‘MOD 26’, instead of writing 26, we go back to 0.
Have a go at coding your name by adding 3 to every letter. Then have a go at coding your name by shifting the alphabet forward by more places by adding greater numbers eg adding 5, then adding 10. Then have a go at decoding. Als je letters getallen zijn en coderen is optellen, dan is decoderen aftrekken, dus als je een bericht hebt gecodeerd door 5 op te tellen, moet je het bericht decoderen door 5 af te trekken.
Redenen!
Als je het coderen van berichten door het alfabet naar voren te schuiven onder de knie hebt, dan heb je je misschien gerealiseerd dat het eigenlijk vrij eenvoudig is om dit type code te kraken. Het kan gemakkelijk worden gedaan door vallen en opstaan. Een vijandelijke codebreker zou slechts 25 verschillende verschuivingen hoeven uit te proberen voordat hij uw berichten kan lezen, wat betekent dat uw berichten niet lang geheim zouden blijven.
Dus, hoe zit het met het coderen van berichten op een andere manier? In plaats van een letter, zouden we een symbool kunnen schrijven, of een tekening maken. In plaats van een ‘A’ zouden we * kunnen schrijven, in plaats van een ‘B’ + enz. Lange tijd dacht men dat zo’n code moeilijk te kraken zou zijn. Het zou de vijand veel te veel tijd kosten om uit te vinden voor welke letter van het alfabet elk symbool stond, gewoon door alle mogelijke combinaties van letters en symbolen uit te proberen. Er zijn 400 miljoen miljard miljard mogelijke combinaties!
Dit type code werd gebruikt door Mary Queen of Scots toen zij een complot smeedde tegen Elizabeth de Eerste. Mary wilde Elizabeth vermoorden, zodat zij zelf koningin van Engeland kon worden, en stuurde dit soort gecodeerde berichten naar haar mede-samenzweerder Anthony Babington. Helaas voor Mary is er een zeer eenvoudige manier om deze code te kraken, zonder vallen en opstaan, maar wel met, surprise, surprise, wiskunde.

Brief verzonden door Mary Queen of Scots aan haar mede-samenzweerder Anthony Babington. Elk symbool staat voor een letter van het alfabet.
Brieven in een taal zijn vrij ongewoon omdat sommige letters vaker worden gebruikt dan andere. Een eenvoudig experiment om dit uit te testen is iedereen in de klas hun hand te laten opsteken als ze de letter ‘E’ in hun naam hebben. Laat vervolgens iedereen met een ‘Z’ zijn hand opsteken, dan een ‘Q’ en dan een ‘A’. U zult waarschijnlijk merken dat ‘E’ en ‘A’ vaker voorkomen dan ‘Z’ en ‘Q’. De grafiek hieronder toont de gemiddelde frequentie van letters in het Engels. Om de informatie samen te stellen, hebben mensen duizenden en duizenden boeken, tijdschriften en kranten doorgekeken, en het aantal keren geteld dat elke letter voorkwam.
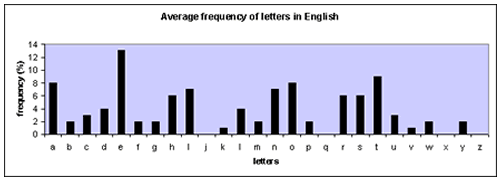
In het Engels is de E de meest gebruikte letter. In een willekeurig stuk schrijven gebruiken we E gemiddeld zo’n 13% van de tijd. T’ is de op een na meest gebruikte letter en ‘A’ is de op twee na meest gebruikte letter.
En het is deze informatie die je kan helpen codes te kraken. Het enige wat de spionnenmeester van Elizabeth de Eerste hoefde te doen om Mary’s code te kraken, was de gecodeerde boodschap door te kijken en het aantal keren te tellen dat elk symbool voorkwam. Het symbool dat het vaakst voorkwam, stond waarschijnlijk voor de letter ‘E’. Kijk naar ons probleem met de Oude Runen voor een andere code die kon worden ontcijferd door te tellen hoe vaak elk symbool voorkwam.
Wanneer je dit soort codes kraakt, door te zoeken naar de meest voorkomende letter, heet dat ‘frequentie-analyse’, en het was deze slimme methode om codes te kraken die ertoe leidde dat Mary haar hoofd werd afgehakt.
Probeer je talenten
Het kraken van deze gecodeerde berichten houdt niet alleen in dat je zoekt naar het meest voorkomende symbool, je kunt ook zoeken naar symbolen die alleen in het bericht voorkomen, d.w.z. één-letter-woorden. Er zijn slechts twee één-letter woorden in het Engels, ‘A’ en ‘I’, dus een een-letter symbool zou moeten staan voor een ‘A’ of ‘I’. Iets anders waar je op kunt letten zijn gewone woorden. De meest voorkomende drieletterwoorden in het Engels zijn ’the’ en ‘and’, dus als je een groep van drie symbolen ziet die vaak voorkomt, zouden ze kunnen staan voor ’the’ of ‘and’.
Als je deze tips voor het breken van codes en je nieuwe codebrekende talenten wilt uitproberen, kijk dan eens naar Simon Singh’s Black Chamber. Het heeft Caesar shift en frequentie analyse puzzels om te breken, en andere codes die je kunt proberen te ontrafelen.
Voor meer informatie over andere geheime codes die door de geschiedenis heen zijn gebruikt, kijk op Simon Singh’s web site. Het staat vol met informatie over allerlei soorten codes, inclusief het beroemde verhaal Enigma, de code machine gebruikt door de Duitsers tijdens de Tweede Wereldoorlog. De Duitsers dachten dat hun code onoverwinnelijk was, maar ongelofelijk genoeg slaagden Britse wiskundigen erin de code te breken en alle berichten te lezen die de Duitsers tijdens de oorlog verstuurden. Historici denken dat deze informatie de oorlog met twee jaar heeft verkort.
WAARSCHUWING
Na het lezen van dit artikel krijg je misschien zin om je eigen codes te verzinnen en je eigen geheime berichten te schrijven. WEES GEWAARSCHUWD. Andere mensen hebben dit artikel ook gelezen en ook zij zullen wiskundige codebrekers van de bovenste plank zijn. Spionnen zijn overal, dus wees voorzichtig – wie leest jouw berichten?
Claire Ellis, de auteur van dit artikel, was directeur van het Enigma Project, dat codes en het breken van codes, en een echte Enigma machine uit de Tweede Wereldoorlog, in het klaslokaal brengt. Voor meer informatie kunt u contact opnemen met de nieuwe directeur, Claire Greer, via de website van het Enigma Schools’ Project.