Magische Vierkanten zijn vierkante rasters met een speciale rangschikking van getallen erin. Deze getallen zijn speciaal omdat elke rij, kolom en diagonaal optelt tot hetzelfde getal. Dus in het voorbeeld hieronder is 15 het magische getal. Kun je dit uitrekenen door alleen te weten dat het vierkant de getallen 1 tot en met 9 gebruikt?

Ook zullen de twee getallen die tegenover elkaar staan tegenover het middelste getal, optellen tot hetzelfde getal. Dus in het vierkant hierboven is 8 + 2 = 10 , 6 + 4 = 10, 1 + 9 = 10 en 3 + 7 = 10. Waarom is dit?
De “volgorde” van een magisch vierkant geeft aan hoeveel rijen of kolommen het heeft. Dus een vierkant met 3 rijen en kolommen is orde 3, en een vierkant met 4 rijen en kolommen is orde 4 enzovoort. Als je meer wilt weten over hoe je je eigen magische vierkanten kunt maken, en de wiskunde achter dit alles, kun je terecht op enkele andere pagina’s op de website, zoals Magische Vierkanten en Magische Vierkanten II.
Maar waarom worden ze magisch genoemd?
De getallen in het Magische Vierkant zijn dus speciaal, maar waarom worden ze magisch genoemd? Het lijkt erop dat ze al vanaf de oudheid verbonden waren met de bovennatuurlijke en magische wereld. De vroegste vermelding van magische vierkanten komt uit China van ongeveer 2200 v. Chr. en wordt “Lo-Shu” genoemd. Volgens een legende zag keizer Yu dit magische vierkant op de rug van een goddelijke schildpad in de Gele Rivier.
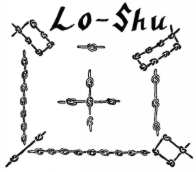
De zwarte knopen tonen even getallen en de witte knopen tonen oneven getallen. Kijk goed en je zult zien dat dit oude magische vierkant hetzelfde is als ons voorbeeld hierboven. Magische vierkanten werden in de Westerse wereld voor het eerst genoemd in het werk van Theon van Smyrna. Ze werden ook gebruikt door Arabische astrologen in de 9e eeuw om te helpen bij het opstellen van horoscopen. Het werk van de Griekse wiskundige Moschopoulos in 1300 n.Chr. hielp de kennis over magische vierkanten te verspreiden. En nu, meer dan 700 jaar later, gebruiken leraren ze in de klas om problemen op te lossen en om te oefenen met optellen.
Je kunt soortgelijke magische vierkanten maken, van orde 3, met verschillende getallen. Zie je patronen in de getallen die werken?