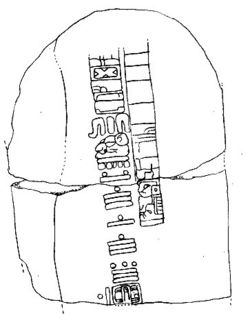
Tres Zapotes Stela – 31 v. Chr.
De Lange Telling, waarvan we de Maya-naam niet kennen, wordt algemeen beschouwd als de lineaire telling van de dagen door de Maya’s. In werkelijkheid is het weer een andere cyclus, maar door de grote lengte van ten minste 5126 jaar is het in wezen een lineaire telling door de hele geschiedenis van de Maya’s heen. De vroegst bekende datum van de Lange Telling, gekerfd in 31 v. Chr., werd gevonden op de Olmec site van Tres Zapotes. De vroegst bekende lange telling van de Maya’s werd opgetekend in het jaar 32 AD op de plaats van Chiapa de Corzo in de hooglanden van Chiapas, Mexico. Net als de christelijke kalender heeft de lange telling een begindatum: de onze is 1 januari 0 AD, en die van hen (volgens onze berekening) 11 augustus 3114 BC. Maar anders dan de onze heeft de hunne ook een schijnbare einddatum, 21 december 2012 n.Chr.
De lange telling wordt weergegeven als een notatiesysteem met vijf plaatsen en oplopende cycli – kins (dagen), winals (maanden van 20 dagen), tuns (360 dagen), k’atuns (20 tuns), en bak’tuns (20 k’atuns). Het is belangrijk op te merken dat de versie van een jaar in de lange telling, de tun, slechts 360 dagen telt, en niet de zonnetelling van 365. Dit betekent dat de lange telling elk jaar vijf dagen afwijkt van de Haab, waardoor het een volledig unieke en aparte cyclus is.

De Vijf Lange Telling Posities
De grootste van de vijf cycli van de lange telling, de bak’tun, is een periode gelijk aan 400 tuns. Veel mensen geloven dat de volledige cyclus van de Lange Telling is voltooid wanneer 13 bak’tuns zijn verstreken sinds het begin van de schepping van dit huidige universum, geïdentificeerd als de 4e schepping in het Maya “scheppingsverhaal”, de Popol Vuh. Die datum, die momenteel van groot belang is voor hen die anticiperen op een “einde der dagen”, zal plaatsvinden op 21 december 2012 AD.
To further illustrate how the Long Count moves forward through time, look at the day sequencing around the beginning and end of the cycle:
| 12.19.19.17.19 | 3 Kawak 7 Kumku | August 10, 3114 BC |
| 13.0.0.0.0 | 4 Ahau 8 Kumku | August 11, 3114 BC |
| 0.0.0.0.1 | 5 Imix 9 Kumku | August 12, 3114 BC |
| 12.19.19.17.19 | 3 Kawak 2 Kankin | December 20, 2012 AD |
| 13.0.0.0.0 | 4 Ahau 3 Kankin | December 21, 2012 AD |
| 0.0.0.0.1 | 5 Imix 4 Kankin | December 22, 2012 AD |
It’s important to point out that this is just one possible scenario for how the Long Count functions and flows. Er zijn andere geleerden die geloven dat de telling niet zou worden teruggezet naar 0.0.0.0.1, maar zou doorgaan met 13 als de bak’tuns, zijnde 13.0.0.0.1, en dan 13.0.0.0.2, enzovoort tot aan de 14e bak’tuns, die wordt weergegeven als 1.0.0.0.0. Lloyd Anderson heeft dit scenario gepresenteerd op zijn website www.traditionalhighcultures.com/MayaMath&WorldAges.html . Aangezien we geen teksten hebben die data presenteren binnen het bereik van de eerste bak’tun van 400 tuns, blijft deze specifieke vraag een academisch debat.
Een andere wijdverbreide overtuiging over de Lange Telling is dat de bak’tun in feite niet wordt teruggezet op 13, maar eerder een andere cyclus van 20 is zoals alle andere plaatswaarden, met uitzondering van de maanden, of winals. De winals zijn 18, en dat komt waarschijnlijk omdat de Maya zonnekalender, de Haab, is verdeeld in 18 maanden van elk 20 dagen. Sir J. Eric Thompson, een van de invloedrijkste Mayaïsten die de kalender ooit heeft bestudeerd, was ervan overtuigd dat de baktuns-cyclus 20 was en niet 13. Hij legde zijn logica uit in het volgende Hij legde zijn logica uit in de volgende passage:
“Ik heb altijd aangenomen dat de bak’tuns niet in 13’s, maar in 20’s waren gegroepeerd, omdat het bewijs voor een vigesimale telling van baktuns in de Dresden en in Palenque en Copan te sterk is om te worden weerlegd. Ik neem aan dat in een vroeg stadium, toen de LC voor het eerst werd uitgevonden, de hoogste periode de baktun was en dat baktuns werden gerangschikt in herhalende reeksen van 13, maar dat een latere wens om het tijdbereik uit te breiden leidde tot de uitvinding van de pictun en nog grotere perioden. Met die uitbreiding van de tijd was het van essentieel belang om de baktuns in een vigesimale telling in te passen. Bijgevolg werden 20 baktuns het equivalent van één pictun, maar tegen die tijd was 4 Ahau 8 Cumku zo sterk ingeburgerd als het eindpunt van een cyclus van 13 baktuns dat het die aanduiding bleef krijgen, hoewel het voor berekeningsdoeleinden als het eindpunt van een cyclus van 20 baktuns werd gerekend”. (Thompson 1960, p 316)
Thompson’s passage brings up an important fact about the long count that is not often discussed – the fact that the Maya recorded higher cycles above the bak’tun. Here are the first few of the known long count cycles above bak’tun:
| Piktun | 20 Bak’tuns | 8000 tuns | 2,880,000 days |
| Kalabtun | 20 Piktuns | 160,000 tuns | 57,600,000 days |
| Kinichiltun | 20 Kalabtuns | 3,200,000 tuns | 1,152,000,000 days |
| Alautun | 20 Kinichiltuns | 64,000,000 tuns | 23,040,000,000 days |
(It should noted that while these are the names for these cycles that have been used in the literature for almost a century, there is no direct evidence that these were their names in ancient times.)
These higher cycles are not uncommon in the inscriptions. Zij komen meerdere malen voor in de Dresden Codex, en in de gebeeldhouwde en geschilderde inscripties van Palenque, Copan, Quirigua, Tikal, Yaxchilan, en Coba. Alleen al het bestaan van deze hogere cycli doet twijfelen aan het idee dat de Lange Telling wordt teruggezet op de 13e bak’tun. Als dat zo zou zijn, waarom zouden deze hogere cycli dan nodig zijn?

Het westpaneel van de Tempel van de Inscripties (tekening door Linda Schele)
Terugkomend op de vraag of de bak’tun plaats vindt in een cyclus van 13 of 20 bak’tuns, is een voorbeeld uit Palenque lange tijd gebruikt om het argument te ondersteunen dat 20 bak’tuns gelijk zijn aan één piktun.
De tekst van het Westelijke Tablet van de Tempel van de Inscripties vermeldt de datum van Pakal’s geboortedag en telt dan ver in de toekomst om uit te komen op 1 piktun.
De tekening rechts toont het gedeelte van de tekst dat hier besproken wordt (tekening door Linda Schele). De rekensom werkt alleen als 20 bak’tuns gelijk zijn aan één piktun. Here’s the progression:
| 9.8.9.13.0 | 8 Ahau 13 Pop | March 24, 603 AD | Pakal’s Birth |
| + | |||
| 10.11.10.5.8 | The text indicates to go this many days into the future | ||
| To arrive at: | |||
| (1.0.0.0.0.8) | 5 Lamat 1 Mol | The text says 1 piktun 8 kins | |
| And then it mentions the calendar round for the date of exactly one piktun: | |||
| (1.0.0.0.0.0) | 10 Ahau 13 Yaxk’in | October 13, 4772 AD | |
One can see how the distance number of 10.11.10.5.8 was chosen very intentionally to get all zeros in the lower order cycles. Als de bak’tun cyclus 13’en had, dan zou de lange telling 1.7.0.0.0.8 zijn geweest, niet 1.0.0.0.8.

Het kruistablet west tekst
tekening door Linda Schele)
Omdat deze teksten over Pakal zo ver in de toekomst gaan, zijn de feiten schaars en de theorieën talrijk. Misschien was het een verklaring over de eeuwige aard van zijn ziel? Of een toekomstige reïncarnatie? Een interessant punt is dat de kalenderronde 5 Lamat 1 Mol ook de datum is van Pakals toetreding in 612 AD, en de 5 Lamat 1 Mol die in de passage wordt genoemd is precies 80 kalenderrondes (52 jaarcycli) later. Aangezien Pakal 80 ton was toen hij stierf, is dit misschien een poëtische uitspraak die zinspeelt op zijn hoge leeftijd.
Als we dus duidelijk bewijs hebben dat de bak’tun cyclus, net als alle andere lange telposities behalve de winals, in cycli van 20 loopt, waarom geloven zo veel mensen dan dat deze zal worden gereset bij de komst van de 13e bak’tun in 2012 AD? Het antwoord ligt in de westerse wiskundige aanname dat als de lange telling begon op 13 bak’tuns, hij dan ook moet eindigen op 13 bak’tuns. Wanneer een persoon uit de westerse cultuur zich een cyclus voorstelt, roept hij onmiddellijk het beeld op van een klok, met een ronddraaiende wijzer die begint en eindigt bij 12. Moet het zo zijn? Een deel van het probleem ligt in de veronderstelling dat de moderne westerse en de oude meso-amerikaanse opvattingen over “cyclus” hetzelfde zijn.
Er zijn inscripties in Palenque, Copan, en Quirigua die specifiek gebeurtenissen dateren van vóór de huidige jaartelling. Zij stellen alle dat zij plaatsvonden binnen de 12e bak’tun en leiden tot 13.0.0.0.0 4 Ahau 8 Kumku. In Palenque stellen de teksten van de Kruisgroep dat op 9 december 3121 v.Chr. een vrouw met de naam Muwan Mat werd geboren. Daarna, 754 jaar na het begin van de jaartelling op 11 augustus 3114 v.Chr. baarde zij op 23 oktober 2360 v.Chr. GI van de Palenque Triade. Deze data omspannen de scheppingsdatum, beginnend in een 12e bak’tun en weer oppakkend in een 1e bak’tun. Here are the long counts in sequential order:
| 12.19.13.4.0 | 8 Ahau 18 Sek | December 9, 3120 BC | Birth of Muwan Mat |
| 13.0.0.0.0 | 4 Ahau 8 Kumku | August 11, 3114 BC | Creation Date |
| 1.18.5.3.7 | 13 Kimi 19 Keh | October 23, 2360 BC | Birth of GI |
These dates are given as full long counts, not abbreviated within distance numbers or implied by calendar rounds. While the evidence is compelling, these few texts from Palenque are almost single handedly responsible for convincing western scholars that the long count will once again reset in 2012 AD.
In point of fact, though we have many instances of the Maya recording 13.0.0.0.0 for August 11, 3114 BC, there is only one text known to record the 13.0.0.0.0 date for December 21, 2012 AD. Deze werd gevonden op Monument 6 uit Tortuguero en de tekst is afgebroken direct nadat de datum is genoemd, waardoor de gebeurtenis waarnaar zou zijn verwezen wordt verduisterd.
Voor de oude Maya’s eindigde de 13e bak’tun aan het begin van de vierde schepping van de wereld, oftewel het tijdperk. De Popol Vuh beschrijft de drie voorgaande scheppingen en het lot van hun bewoners, maar geeft geen data. De Azteken hadden een zeer vergelijkbaar concept en legden het aan de Spanjaarden in enig detail uit. Voor de Azteken leefden zij in het 5e wereldtijdperk, niet het 4e. Mark Van Stone (persoonlijke communicatie 2008) veronderstelt dat de Azteken de ineenstorting van de klassieke Maya beschaving in de 9e eeuw tot het einde van de 4e schepping gerekend zouden kunnen hebben.
De Azteken gaven tijdslengtes voor elk van de voorgaande tijdperken en, zeer belangrijk, zij waren niet hetzelfde. Hier zijn de vier Azteekse tijdperken vóór het huidige:
| The first era | 13 cycles of 52 years for a total of 676 years |
| The second era | 7 cycles of 52 years for a total of 364 years |
| The third era | 6 cycles of 52 years for a total of 312 years |
| The fourth era | 13 cycles of 52 years for a total of 676 years |

The Aztec Calendar Stone (National Antropology Museum, Mexico DF)
If one lumps the 2nd and 3rd era time lengths together, they get another set of 13 x 52 years, just like the 1st and 4th eras. Like the Maya, the Aztec seem to have related the concept of 13 cycles with the completion of an era or world creation. The current era was not given a time length, but was predicted by the Aztecs to be ultimately destroyed by earthquakes. Given the difference in past cycle lengths, one could not safely assume that the current Aztec era will be 13 x 52 years. Geldt deze zelfde voorzichtigheid niet voor het Maya-begrip van de lengte van een jaartelling?
Een deel van de oplossing kan liggen in het onderscheiden van het conceptuele verschil tussen een “cyclus” en een “jaartelling”. Er zijn wel degelijk vaste cycli in de gehele Mayakalender, en de in elkaar grijpende aard ervan is ervan afhankelijk. De kin, de tun, de winal en de k’atun zijn allemaal statische cycli van tijd. De westerse kalender kent dezelfde soort cyclische incrementen – een dag, een jaar, een eeuw, een millennium, enz. Een “tijdperk” in het westerse denken is echter zelden een exacte increment van een calendrische cyclus. De IJzertijd, de Renaissance, het Industrialisme – elk van deze was een ander “tijdperk” in de geschiedenis met een unieke tijdsduur. Drukten de Maya’s hetzelfde conceptuele verschil uit toen zij schreven dat 13 bak’tuns het einde van een tijdperk was? Er is reden om aan te nemen dat het getal 13 werd gebruikt als een symbolische manier om “voltooiing” te zeggen. Er zijn teksten in Yaxchilan, Coba, en de Dresden Codex die lange teldatums presenteren waarin vele cycli boven de bak’tun het getal 13 herhalen als hun coëfficiënten. Het voorbeeld in Yaxchilan, op een paneel voor Tempel 33, plaatst tien 13’en boven een hedendaagse datum:
| 13.13.13.13.13.13.13.13.9.15.13.6.9 | Oct 19, 744 AD |
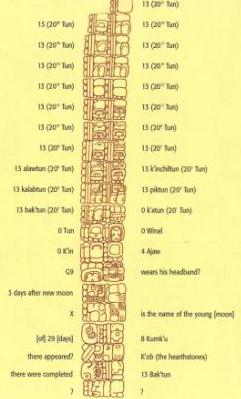
Coba Stela 1
(tekening naar Elizabeth Wagner)
Het voorbeeld in Coba, op Stela 1, plaatst minstens twintig 13’en boven de scheppingsdatum, 13.0.0.0.0 11 augustus, 3314 v.Chr. Als we zouden proberen al die 13’s te tellen als werkelijke coëfficiënten, elk met een grootte van 20, dan zou de datum die we zouden krijgen 41.943.040.000.000.000.000.000.000.000.000.000 jaar in het verleden liggen! Dresden Codex pagina 52 vermeldt ook een datum met 13 opeenvolgende 13’s. Aangezien geen van deze 13’en van invloed is op de lagere cycli, lijkt het er niet op dat ze daar zijn geplaatst om daadwerkelijk te worden berekend. Ze zijn waarschijnlijk meer een symbolische verklaring dat er vele cycli zijn verstreken. Als deze coëfficiënten van 13 voor de piktuns, kalabtun, kinichiltuns, enz… dagen lang geleden symboliseren, zouden 13 bak’tuns dan niet hetzelfde kunnen symboliseren?
Dus, als het idee dat de 13e Bak’tun het einde van de huidige jaartelling betekent in twijfel wordt getrokken, wat moeten we dan denken van de komst ervan in 2012 AD? Hoewel Mayateksten niets zeggen over wat er zou kunnen gebeuren bij de 13e Bak’tun, weten we wel dat het einde van elke Bak’tun werd beschouwd als een tijd van grote verandering. Bestudering van de oude Maya geschiedenis geeft een algemene bevestiging van dat begrip.
De volgende gebeurtenissen rond de wisseling van de laatste vijf bak’tuns zijn niet bedoeld als exacte data waarop grote veranderingen plaatsvonden, maar als een algemeen patroon.
Het begin van de 8e bak’tun (41 AD)
De laatste Olmeekse steden, waarvan sommige bijna 1000 jaar hadden bestaan, werden verlaten en nooit meer bewoond.
Het begin van de 9e bak’tun (435 n.Chr.)
De invloed van Teotihuacan begon in de Maya-wereld, met als gevolg nieuwe steden, een vlaag van nieuwe dynastieën, en oorlogsvoering.
Het begin van de 10e bak’tun (830 na Chr.)
Het einde van de Klassieke periode en de nog steeds onverklaarbare leegloop van 100’en steden.
Het begin van de 11e bak’tun (1224 na Chr.)
De leegloop van Chichen Itza in Yucatan en de opkomst van Mayapan.
Het begin van de 12e bak’tun (1618 na Chr.)
Het laatste grote Maya-rijk, de Itza van het Petenmeer, stuurde afgezanten naar de Spanjaarden om aan te kondigen dat zij klaar zijn om de verandering te omarmen die de omwenteling van de cycli zal brengen.
Het was deze laatste bak’tun, toen de Spanjaarden het Petenmeer veroverden en koning Kan Ek gevangennamen, die een bijzonder inzicht verschaft in de Maya geloofsovertuigingen over de omwenteling van een bak’tun. In het jaar 1617 zond Kan Ek afgezanten naar Merida om de Spanjaarden te informeren dat de 12e bak’tun nabij was en dat zij voorbereid waren op de verandering die deze zou brengen. De Spanjaarden interpreteerden dit als een bereidheid om zich tot het christendom te laten bekeren en er begon een wedloop tussen verschillende zendelingen om de eer om als eerste de machtige Itza te bekeren. Met de priesters kwamen de soldaten, en het onvermijdelijke einde. Hoewel de Itza zeker niet hun eigen ondergang planden, hadden ze wel gelijk dat er een tijd van grote veranderingen voor de deur stond.
Ter afsluiting: hoewel het niet zeker is dat 2012 n.Chr. het begin zal zijn van de lange telcyclus, is het wel degelijk het begin van de 13e bak’tun. De oude Maya’s zouden het als een tijd van grote verandering hebben beschouwd. Als elke bak’tun een tijd van grote verandering was, dan moet de 13e draai een speciale betekenis hebben gehad, misschien wel het begin van een nieuw tijdperk in de wereldgeschiedenis. De tijd zal het leren.
De Maya kalender zal een bron van veel fascinatie blijven, en mensen aanzetten tot het schrijven van boeken en films over de heraldische datum in 2012. Hoewel de huidige computers of o2 mobiele telefoons christelijke kalenders hebben, zal de Maya cultuur bij ons blijven, zelfs nadat al dan niet bewezen is dat deze verouderd is. Wij hopen dat u genoten hebt van dit artikel, en natuurlijk, als u gedachten of opmerkingen hebt over of over de besproken informatie, aarzel dan niet om contact op te nemen.