Projecties
Nu wij het concept van dimensieverkleining en enkele toepassingen van SVD en principale componentenanalyse hebben beschreven, gaan wij dieper in op de details van de wiskunde daarachter. We beginnen met projecties. Een projectie is een lineair algebra-concept dat ons helpt om veel van de wiskundige operaties te begrijpen die we uitvoeren op hoog-dimensionale gegevens. Voor meer details kunt u projecties nalezen in een lineaire algebra boek. Hier geven we een kort overzicht en vervolgens enkele aan data-analyse gerelateerde voorbeelden.
Als overzicht, onthoud dat projecties de afstand tussen punten en deelruimte minimaliseren.

In de figuur hierboven wijst het punt bovenaan naar een punt in de ruimte. In dit specifieke beeldverhaal is de ruimte tweedimensionaal, maar we moeten abstract denken. De ruimte wordt voorgesteld door het cartesiaanse vlak en de lijn waarop het persoontje staat is een deelruimte van punten. De projectie naar deze deelruimte is de plaats die het dichtst bij het oorspronkelijke punt ligt. Meetkunde vertelt ons dat we dit dichtstbijzijnde punt kunnen vinden door een loodrechte lijn (stippellijn) van het punt naar de ruimte te laten vallen. Het persoontje staat op de projectie. De afstand die dit persoontje heeft moeten lopen van de oorsprong naar het nieuwe geprojecteerde punt noemen we de coördinaat.
Voor de uitleg van projecties zullen we de standaard matrixalgebra-notatie voor punten gebruiken: is een punt in de -dimensionale ruimte en is kleinere deelruimte.
Eenvoudig voorbeeld met N=2
Als we . We kunnen het als volgt plotten:
mypar (1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)text(2,3," Y",pos=4,cex=3)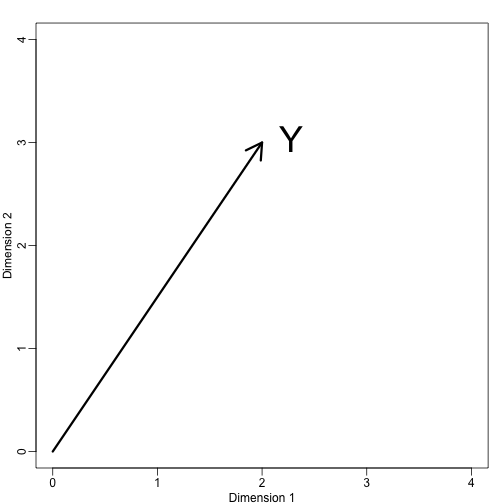
We kunnen onmiddellijk een coördinatenstelsel definiëren door deze vector te projecteren op de ruimte gedefinieerd door: (de x-as) en (de y-as). De projecties van naar de deelruimte gedefinieerd door deze punten zijn respectievelijk 2 en 3:
We zeggen dat en de coördinaten zijn en dat de bases zijn.
Laten we nu een nieuwe deelruimte definiëren. De rode lijn in de plot hieronder is deelruimte gedefinieerd door punten die voldoen aan . De projectie van onto is het dichtstbijzijnde punt op . We moeten dus de vinden die de afstand tussen en minimaliseert. In de lineaire algebra leren we dat het verschil tussen deze punten loodrecht op de ruimte staat, dus:
Dit impliceert dat:
en:
Hier staat de punt voor het dotproduct: .
De volgende R-code bevestigt dat deze vergelijking werkt:
mypar(1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)abline(0,0.5,col="red",lwd=3) #if x=2c and y=c then slope is 0.5 (y=0.5x)text(2,3," Y",pos=4,cex=3)y=c(2,3)x=c(2,1)cc = crossprod(x,y)/crossprod(x)segments(x*cc,x*cc,y,y,lty=2)text(x*cc,x*cc,expression(hat(Y)),pos=4,cex=3)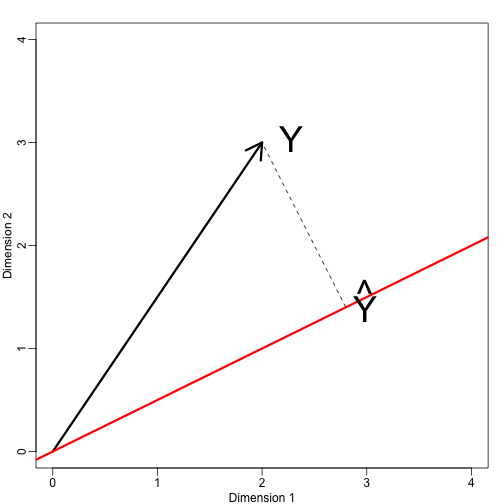
Merk op dat als was zodanig dat , dan is eenvoudig en de ruimte verandert niet. Deze vereenvoudiging is een van de redenen waarom we van orthogonale matrices houden.
Voorbeeld: Het steekproefgemiddelde is een projectie
Laat en is de ruimte overspannen door:
In deze ruimte zijn alle componenten van de vectoren hetzelfde getal, zodat we kunnen denken aan deze ruimte als representanten van de constanten: in de projectie zal elke dimensie dezelfde waarde hebben. Dus wat minimaliseert de afstand tussen en ?
Wanneer we het over dit soort problemen hebben, gebruiken we soms tweedimensionale figuren, zoals de figuur hierboven. We abstraheren gewoon en denken aan een punt in en als deelruimte gedefinieerd door een kleiner aantal waarden, in dit geval slechts één: .
Terugkomend op onze vraag, weten we dat de projectie is:
wat in dit geval het gemiddelde is:
Hier zou het ook net zo gemakkelijk zijn geweest om calculus te gebruiken:
Voorbeeld: Regressie is ook een projectie
Laten we een iets gecompliceerder voorbeeld geven. Eenvoudige lineaire regressie kan ook worden verklaard met projecties. Onze gegevens (we gaan de notatie niet meer gebruiken) zijn weer een vector en ons model voorspelt met een lijn . We want to find the and that minimize the distance between and the space defined by:
with:
Our matrix is and any point in can be written as .
The equation for the multidimensional version of orthogonal projection is:
which we have seen before and gives us:
And the projection to is therefore: