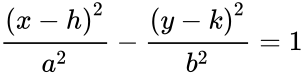by: adminPosted on:

Semi-major axis

File:Semimajoraxis.png

De halve lange as van een ellips

In de meetkunde wordt de term halve lange as (ook halve lange as) gebruikt om de afmetingen van ellipsen en hyperbolen te beschrijven.

Ellips

De hoofdas van een ellips is de langste diameter, een lijn die door het middelpunt en beide brandpunten loopt en waarvan de uiteinden op de breedste punten van de vorm liggen. De halve lange as is de helft van de lange as, en loopt dus van het middelpunt, door een brandpunt, naar de rand van de ellips.

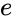
Hij is gerelateerd aan de halve korte as {displaystyle b,\!} door de excentriciteit {displaystyle e,\!} en het semi-latus rectum {\displaystyle \ell \,\!}, als volgt:

{\displaystyle b=a{\sqrt {1-e^{2}}},\!}{\displaystyle \ell =a(1-e^{2})\,\!}{Displaystyle aell =b^{2},\!}.

Een parabool kan worden verkregen als de limiet van een reeks ellipsen waarbij het ene brandpunt vast blijft en het andere willekeurig ver weg mag bewegen in één richting, waarbij {\displaystyle \ell \,\!} vast blijft. Dus {\displaystyle a,\!} en {\displaystyle b,\!} neigen naar oneindig, {\displaystyle a,\!} sneller dan {\displaystyle a,\!}. sneller dan {\displaystyle b,}.

De halve lange as is de gemiddelde waarde van de kleinste en grootste afstanden van een brandpunt tot de punten op de ellips. Beschouw nu de vergelijking in poolcoördinaten, met het ene brandpunt op de oorsprong en het andere op de positieve x-as,

{\displaystyle r(1-ecos \theta )=l\,\!}

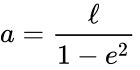
The mean value of {\displaystyle r={\ell \over {1+e}}\,\!} and {\displaystyle r={\ell \over {1-e}}\,\!}, is {\displaystyle a={\ell \over {1-e^{2}}}\,\!}.

Hyperbola

The semi-major axis of a hyperbola is one half of the distance between the two branches; if this is a in the x-direction the equation is:

{\displaystyle {\frac {\left(x-h\right)^{2}}{a^{2}}}-{\frac {\left(y-k\right)^{2}}{b^{2}}}=1}

In terms of the semi-latus rectum and the eccentricity we have

{\displaystyle a={\ell \over e^{2}-1}}

Astronomy

Orbital period

In astrodynamics the orbital period 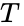{\displaystyle T\,} of a small body orbiting a central body in a circular or elliptical orbit is:

{\displaystyle T=2\pi {\sqrt {a^{3}/\mu }}}

where:

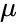
{\displaystyle a,}is de lengte van de halve lange as van de baan{\displaystyle \mu }is de standaard gravitatieparameter

Merk op dat voor alle ellipsen met een gegeven halve lange as de omlooptijd hetzelfde is, ongeacht de excentriciteit.

In de astronomie is de halve lange as een van de belangrijkste baanelementen van een baan, samen met de baanperiode. Voor objecten in het zonnestelsel is de halve lange as gerelateerd aan de periode van de baan door de derde wet van Kepler (oorspronkelijk empirisch afgeleid),

{\displaystyle T^{2}=a^{3}\,}

waarbij T de periode in jaren is, en a de halve lange as in astronomische eenheden. Deze vorm blijkt een vereenvoudiging te zijn van de algemene vorm voor het tweelichamenprobleem, zoals bepaald door Newton:

{Displaystyle T^{2}={\frac {4pi ^{2}{G(M+m)}}a^{3},}

waarin G de gravitatieconstante is, en M de massa van het centrale lichaam, en m de massa van het omcirkelende lichaam. Gewoonlijk is de massa van het centrale lichaam zoveel groter dan die van het hemellichaam, dat m kan worden verwaarloosd. Door die aanname te doen en typische astronomische eenheden te gebruiken, ontstaat de eenvoudigere vorm die Kepler ontdekte.

Het is opmerkelijk dat het pad van het hemellichaam rond het zwaartepunt en zijn pad ten opzichte van zijn primaire hemellichaam beide ellipsen zijn. De halve lange as die in de astronomie wordt gebruikt, is altijd de afstand tussen de primaire en de secundaire as; de baanparameters van de planeten worden dus in heliocentrische termen gegeven. Het verschil tussen de primocentrische en “absolute” banen kan het best worden geïllustreerd aan de hand van het Aarde-Maan systeem. De massaverhouding is in dit geval 81,30059. De karakteristieke afstand aarde-maan, de halve lange as van de geocentrische maanbaan, is 384.400 km. De barycentrische maanbaan heeft daarentegen een halve lange as van 379.700 km, waarbij de tegenbaan van de aarde het verschil, 4.700 km, opvangt. De gemiddelde barycentrische omloopsnelheid van de maan is 1,010 km/s, terwijl die van de aarde 0,012 km/s is. Het totaal van deze snelheden geeft de geocentrische gemiddelde omloopsnelheid van de maan, 1,022 km/s; dezelfde waarde kan worden verkregen door alleen naar de geocentrische halve lange as waarde te kijken.

Gemiddelde afstand

Vaak wordt gezegd dat de halve lange as de “gemiddelde” afstand is tussen de primaire (het brandpunt van de ellips) en het hemellichaam in de baan. Dit is niet helemaal juist, want het hangt ervan af waarover het gemiddelde wordt genomen.

  • Het middelen van de afstand over de excentrische anomalie (q.v.) levert inderdaad de semi-majooras op.
  • gemiddeld over de ware anomalie (de ware baanhoek, gemeten bij het brandpunt) levert, vreemd genoeg, de halve lange as op {\displaystyle b=a{\sqrt {1-e^{2}}},\!
  • gemiddeld over de gemiddelde anomalie (het deel van de omlooptijd dat sinds het pericentrum is verstreken, uitgedrukt in een hoek) geeft tenslotte het tijdgemiddelde (wat “gemiddelde” voor de leek meestal betekent): {\displaystyle a(1+{\frac {e^{2}}{2}})\,\.

Het tijdgemiddelde van de inverse van de straal, {\displaystyle r^{-1},\!}, is {\displaystyle a^{-1},\!}.

Energie; berekening van halve lange as uit toestandsvectoren

In de astrodynamica kan de halve lange as {\displaystyle a^{-1},} worden berekend uit de toestandsvectoren van de banen:

{\displaystyle a={-\mu \over {2\epsilon }}\,} for an elliptical orbit and {\displaystyle a={\mu \over {2\epsilon }}\,} for a hyperbolic trajectory

and

{\displaystyle \epsilon ={v^{2} \over {2}}-{\mu \over \left|\mathbf {r} \right|}} (specific orbital energy)

and

{\displaystyle \mu =GM\,} (standard gravitational parameter),

where:

  • {\displaystyle v\,} is orbital velocity from velocity vector of an orbiting object,
  • {\displaystyle \mathbf {r} \,} is cartesian position vector of an orbiting object in coordinates of a reference frame with respect to which the elements of the orbit are to be calculated (e.g. geocentrisch equatoriaal voor een baan rond de aarde, of heliocentrisch ecliptisch voor een baan rond de zon),
  • {displaystyle G,} is de gravitatieconstante,
  • {displaystyle M,} de massa van het centrale lichaam.

Merk op dat voor een gegeven centraal hemellichaam en totale specifieke energie, de halve lange as altijd gelijk is, ongeacht de excentriciteit. Omgekeerd is voor een gegeven centraal lichaam en halve lange as de totale specifieke energie altijd gelijk.

Voorbeeld

Het internationale ruimtestation heeft een omlooptijd van 91,74 minuten, de halve lange as is dus 6738 km . Elke minuut meer komt overeen met ca. 50 km meer: de extra 300 km baanlengte kost 40 seconden, de lagere snelheid is goed voor 20 seconden extra.

Geef een antwoord

Het e-mailadres wordt niet gepubliceerd. Vereiste velden zijn gemarkeerd met *