Teoria MO i sprzężone wiązania pi
Zaleta stosowania teorii MO do zrozumienia wiązań w cząsteczkach organicznych staje się bardziej oczywista, gdy myślimy o wiązaniach pi. Rozważmy najpierw wiązanie pi w etenie z punktu widzenia teorii MO (w tym przykładzie pominiemy wiązania s w cząsteczce i będziemy myśleć tylko o wiązaniu π). Zaczynamy od dwóch orbitali atomowych: po jednym niehybrydyzowanym orbitalu 2p z każdego węgla. Każdy z nich zawiera pojedynczy elektron. W teorii MO, te dwa atomowe łączą się matematycznie tworząc dwa orbitale pi molekularne, jeden niskoenergetyczny orbital wiązania pi i jeden wysokoenergetyczny orbital wiązania pi*.
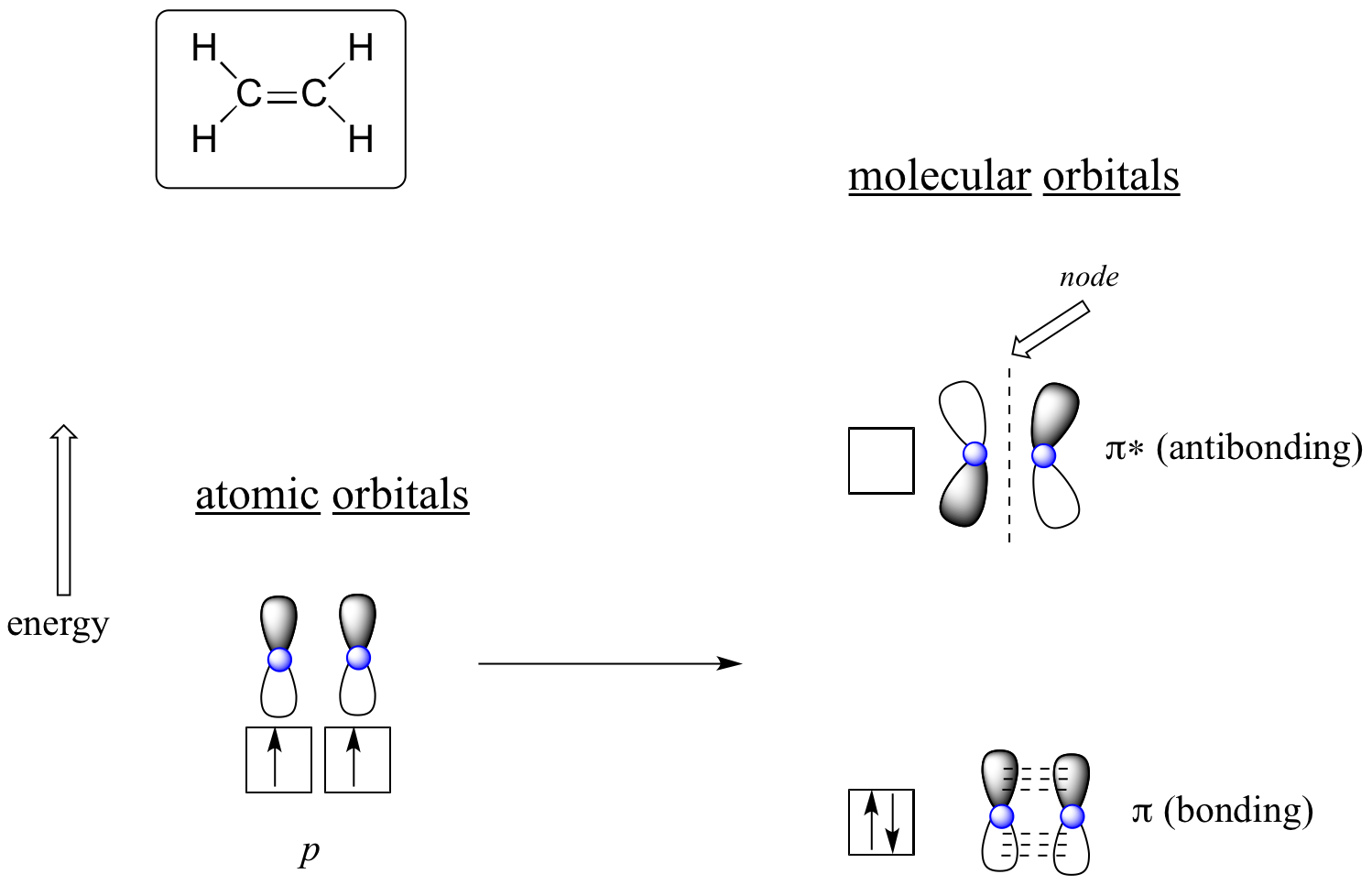
Orbitale molekularne dla etenu (etylenu)
W orbitalu wiążącym pi, dwa zacienione płaty orbitali p oddziałują ze sobą konstruktywnie, podobnie jak dwa niezacienione płaty (pamiętajmy, że arbitralny wybór cieniowania reprezentuje matematyczne znaki (+) i (-) dla matematycznej funkcji falowej opisującej orbital). Pomiędzy dwoma jądrami węgla na orbitalu molekularnym występuje zwiększona gęstość elektronów – jest to oddziaływanie wiążące.
W wyżejenergetycznym antywiązaniowym orbitalu pi*, zacieniony płat jednego orbitalu p oddziałuje destrukcyjnie z niezacienionym płatem drugiego orbitalu p, prowadząc do powstania węzła pomiędzy dwoma jądrami i ogólnego odpychania pomiędzy jądrami węgla.
Ponownie stosując zasadę „budowania”, umieszczamy dwa elektrony w niżej energetycznym, wiążącym orbitalu molekularnym pi. Przeciwwiązaniowy orbital pi* pozostaje pusty.
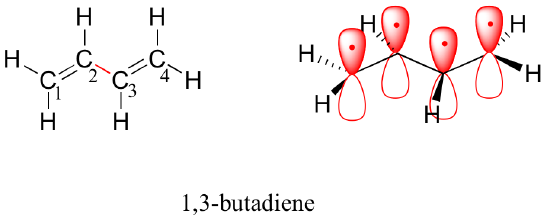
Następnie rozważymy cząsteczkę 1,3-butadienu. Na podstawie samej teorii orbitali walencyjnych można by się spodziewać, że wiązanie C2-C3 w tej cząsteczce, ponieważ jest to wiązanie sigma, będzie mogło się swobodnie obracać.

Doświadczalnie jednak zaobserwowano, że istnieje znaczna bariera dla rotacji wokół wiązania C2-C3, a cała cząsteczka jest planarna. Ponadto, wiązanie C2-C3 ma długość 148 pm, czyli jest krótsze niż typowe pojedyncze wiązanie węgiel-węgiel (ok. 154 pm), ale dłuższe niż typowe wiązanie podwójne (ok. 134 pm).
Teoria orbitali molekularnych wyjaśnia te obserwacje za pomocą koncepcji zdelokalizowanych wiązań pi. W tym obrazie, cztery orbitale atomowe 2p łączą się matematycznie, tworząc cztery orbitale molekularne pi o rosnącej energii. Dwa z nich – wiążące orbitale pi – mają niższą energię niż orbitale atomowe p, z których zostały utworzone, podczas gdy dwa – wiążące orbitale pi* – mają wyższą energię.

Najniżej energetyczny orbital molekularny, pi1, ma tylko konstruktywne oddziaływanie i zero węzłów. Wyższy w energii, ale wciąż niższy niż izolowane orbitale p, orbital pi2 ma jeden węzeł, ale dwa konstruktywne oddziaływania – jest to więc wciąż orbital wiążący. Patrząc na dwa orbitale wiążące, pi3* ma dwa węzły i jedno konstruktywne oddziaływanie, podczas gdy pi4* ma trzy węzły i zero konstruktywnych oddziaływań.
Zgodnie z zasadą aufbau, cztery elektrony z izolowanych orbitali atomowych 2pz są umieszczone w wiążących orbitalach pi1 i pi2 MO. Ponieważ pi1 zawiera konstruktywne oddziaływania pomiędzy C2 i C3, w cząsteczce 1,3-butadienu istnieje pewien stopień oddziaływań wiązania pi- pomiędzy tymi dwoma węglami, co odpowiada za jej mniejszą długość i barierę rotacji. Obraz wiązania walencyjnego 1,3-butadienu przedstawia dwa wiązania pi jako odizolowane od siebie, z każdą parą elektronów pi „zakleszczoną” w swoim własnym wiązaniu pi. Jednakże, teoria orbitali molekularnych przewiduje (dokładnie), że cztery elektrony pi są w pewnym stopniu zdelokalizowane, lub 'rozproszone’, w całym systemie pi.
widok wypełniający przestrzeń
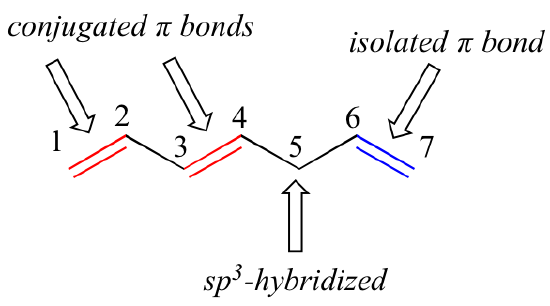
1,3-butadien jest najprostszym przykładem systemu sprzężonych wiązań pi. Aby dwa lub więcej wiązań pi można było uznać za sprzężone, muszą one być rozdzielone tylko jednym wiązaniem pojedynczym – innymi słowy, nie może być pomiędzy nimi węgla hybrydyzującego sp3, ponieważ rozerwałoby to nakładający się układ równoległych orbitali p. W poniższym związku, na przykład, wiązania podwójne C1-C2 i C3-C4 są sprzężone, podczas gdy wiązanie podwójne C6-C7 jest odizolowane od pozostałych dwóch wiązań pi przez sp3-hybrydyzowany węgiel C5.
Bardzo ważną koncepcją, o której należy pamiętać jest to, że istnieje nieodłączna stabilność termodynamiczna związana z koniugacją. Stabilność ta może być zmierzona doświadczalnie poprzez porównanie ciepła uwodornienia dwóch różnych dienów. (Uwodornienie jest typem reakcji, o którym dowiemy się więcej w rozdziale 15: zasadniczo jest to proces dodawania cząsteczki wodoru – dwóch protonów i dwóch elektronów – do wiązania p). Kiedy dwa sprzężone wiązania podwójne 1,3-pentadienu są „uwodornione” w celu wytworzenia pentanu, na każdy mol powstałego pentanu uwalniane jest około 225 kJ. Porównaj to z około 250 kJ/mol uwolnionymi podczas uwodornienia dwóch izolowanych wiązań podwójnych w 1,4-pentadienie, również tworzących pentan.
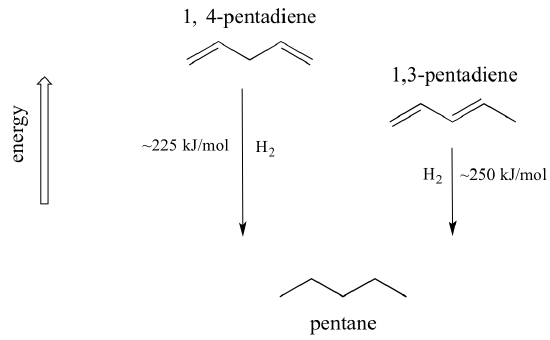
Sprzężony diene ma niższą energię: innymi słowy, jest bardziej stabilny. Ogólnie rzecz biorąc, skoniugowane wiązania pi są bardziej stabilne niż izolowane wiązania pi.
Skoniugowane układy pi mogą obejmować atomy tlenu i azotu, jak również węgla. W metabolizmie cząsteczek tłuszczu niektóre z kluczowych reakcji zachodzą z udziałem alkenów, które są sprzężone z grupami karbonylowymi.

W rozdziale 4 zobaczymy, że teoria MO jest bardzo użyteczna w wyjaśnianiu, dlaczego cząsteczki organiczne, które zawierają rozbudowane układy sprzężonych wiązań pi, często mają charakterystyczne kolory. beta-karoten, związek odpowiedzialny za pomarańczowy kolor marchewki, ma rozbudowany system 11 sprzężonych wiązań pi.
Ćwiczenie: Zidentyfikuj wszystkie sprzężone i izolowane wiązania podwójne w poniższych strukturach. Dla każdego sprzężonego układu pi podaj liczbę nakładających się na siebie orbitali p oraz ile elektronów pi jest między nimi współdzielonych.
Ćwiczenie: Zidentyfikuj wszystkie izolowane i sprzężone wiązania pi w likopenie, związku o czerwonej barwie występującym w pomidorach. Ile elektronów pi znajduje się w sprzężonym układzie pi?

Rozwiązania do ćwiczeń
Aromatyczność – ostateczny układ sprzężony
Teoria orbitali molekularnych jest szczególnie pomocna w wyjaśnianiu unikalnych właściwości związków aromatycznych, takich jak benzen:
3D interaktywny model benzenu
Mimo, że benzen najczęściej rysowany jest z trzema wiązaniami podwójnymi i trzema pojedynczymi, w rzeczywistości wszystkie wiązania węgiel-węgiel mają dokładnie taką samą długość (138 pm). Ponadto, wiązania pi w benzenie są znacznie mniej reaktywne niż „normalne” wiązania pi, zarówno izolowane jak i sprzężone. Coś w strukturze benzenu sprawia, że jego układ wiązań pi jest szczególnie stabilny. To „coś” ma swoją nazwę: nazywa się to „aromatycznością”.
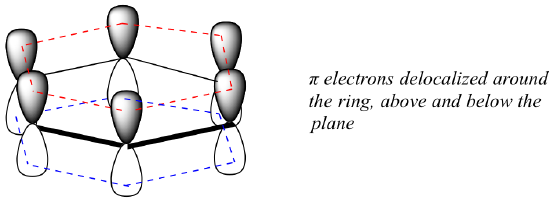
Co dokładnie jest tą „aromatyczną” właściwością, która sprawia, że wiązania pi w benzenie są tak stabilne? W dużej mierze odpowiedź na to pytanie leży w fakcie, że benzen jest cząsteczką cykliczną, w której wszystkie atomy pierścienia są sp2-hybrydyzowane. Pozwala to na delokalizację elektronów pi na orbitale molekularne, które rozciągają się wokół całego pierścienia, powyżej i poniżej płaszczyzny. Aby tak się stało, pierścień musi być oczywiście planarny – w przeciwnym razie orbitale p nie mogłyby się prawidłowo nakładać. Benzen jest rzeczywiście znany jako płaska cząsteczka.
Czy wszystkie cykliczne cząsteczki z naprzemiennymi wiązaniami pojedynczymi i podwójnymi mają taką samą stabilność aromatyczną? Odpowiedź w rzeczywistości brzmi „nie”. Ośmioczłonowy pierścień cyklooktatetraenu pokazany poniżej nie jest płaski, a jego wiązania π reagują jak „normalne” alkeny.
Wyraźnie potrzeba czegoś więcej, aby być aromatycznym, a to można najlepiej wyjaśnić za pomocą teorii orbitali molekularnych. Spójrzmy na diagram energetyczny orbitali molekularnych pi w benzenie.
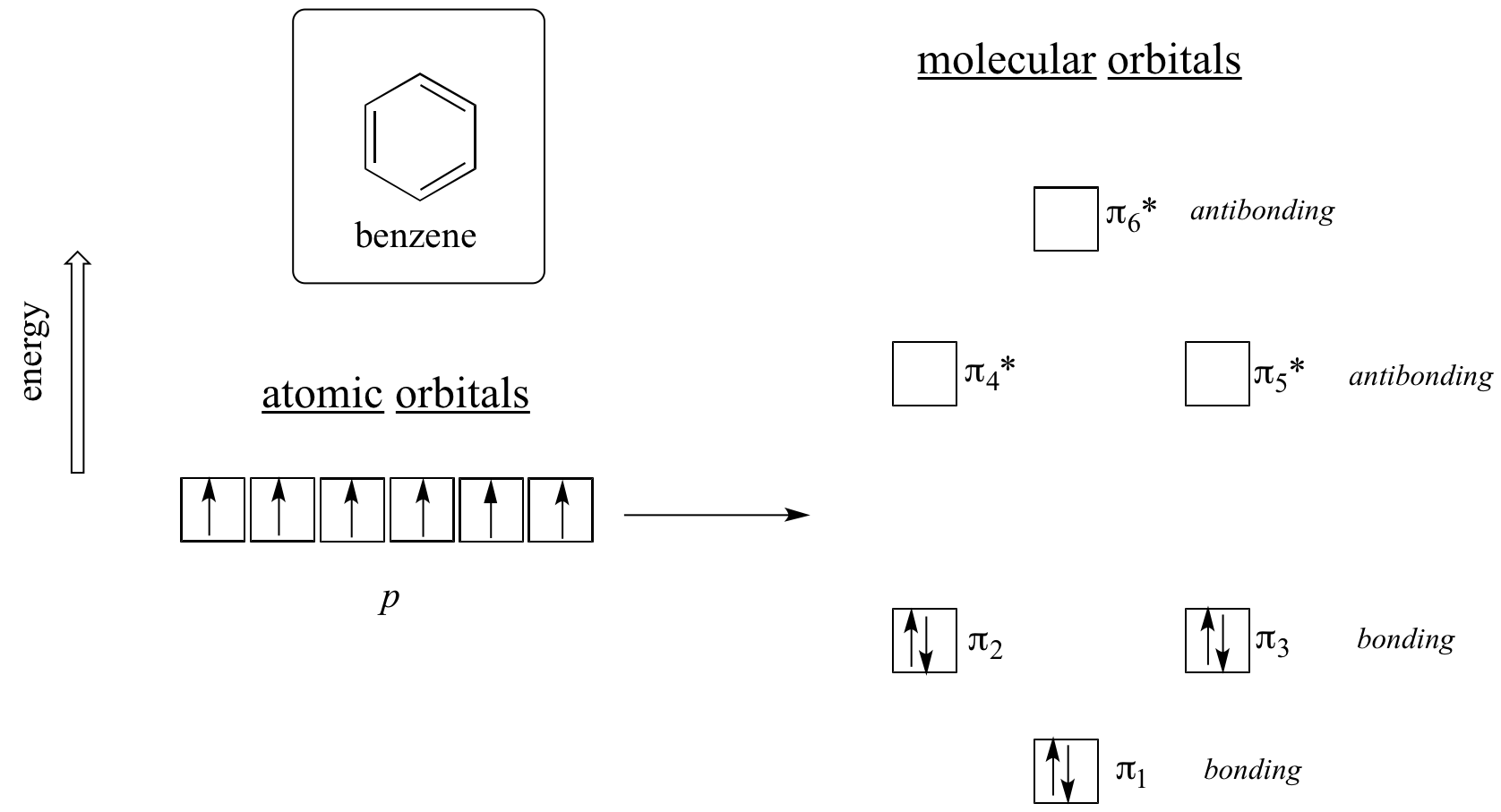
Obliczenia mechaniki kwantowej mówią nam, że sześć orbitali molekularnych pi w benzenie, utworzonych z sześciu atomowych orbitali p, zajmuje cztery oddzielne poziomy energetyczne. pi1 i pi6* mają unikalne poziomy energetyczne, podczas gdy pary pi2 – pi3 i pi4* – pi5* są zdegenerowane, co oznacza, że znajdują się na tym samym poziomie energetycznym. Kiedy użyjemy zasady aufbau, aby wypełnić te orbitale sześcioma elektronami pi w benzenie, zobaczymy, że orbitale wiążące są całkowicie wypełnione, a orbitale przeciw wiązaniom są puste. To daje nam dobrą wskazówkę co do źródła szczególnej stabilności benzenu: pełny zestaw wiążących MO jest podobny na wiele sposobów do „pełnej powłoki” elektronów w orbitalach atomowych stabilnych gazów szlachetnych: helu, neonu i argonu.
Zróbmy to samo dla cyklooktatetraenu, który jak już wiemy nie jest aromatyczny.
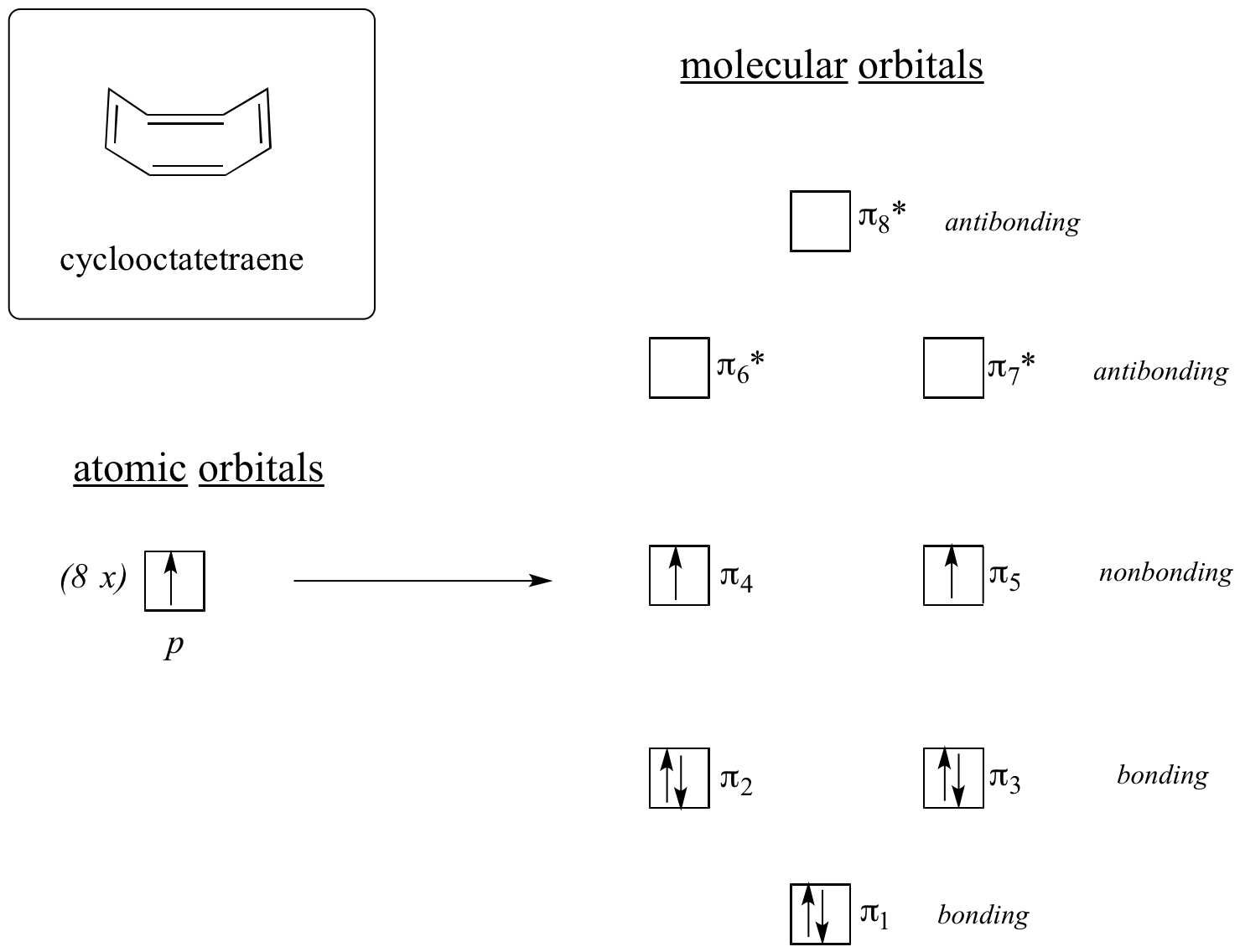
Wynik obliczeń orbitali molekularnych mówi nam, że najniższa i najwyższa energia MO (pi1 i pi8*) mają unikalne poziomy energetyczne, podczas gdy pozostałe sześć tworzą zdegenerowane pary. Zauważmy, że pi4 i pi5 są na tym samym poziomie energetycznym co izolowane orbitale atomowe 2pz: nie są to zatem ani wiązania ani przeciwwiązania, a raczej są one określane jako niewiążące MO. Wypełniając MO ośmioma elektronami pi w cząsteczce, stwierdzamy, że dwa ostatnie elektrony są niesparowane i przypadają na dwa zdegenerowane orbitale niezwiązane. Ponieważ nie mamy idealnie wypełnionej powłoki wiążących MO, nasza cząsteczka nie jest aromatyczna. W konsekwencji, każde z wiązań podwójnych w cyklooktatetraenie zachowuje się bardziej jak izolowane wiązanie podwójne.
Na razie ważnym celem nauki jest rozpoznanie sprzężonych układów wiązań pi i zrozumienie, że benzen jest wyjątkowo stabilny, wykazując właściwość zwaną aromatycznością. Aromatyczność i chemia związków aromatycznych jest stosunkowo złożona i jest omówiona bardziej szczegółowo w kolejnych rozdziałach tego tekstu.
Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)