W naszej dyskusji na temat przedziału ufności dla \u_{Y}, użyliśmy wzoru, aby zbadać, jakie czynniki wpływają na szerokość przedziału ufności. Nie ma potrzeby robić tego ponownie. Ponieważ wzory są tak podobne, okazuje się, że czynniki wpływające na szerokość przedziału predykcji są identyczne z czynnikami wpływającymi na szerokość przedziału ufności.
W zamian zbadajmy wzór na przedział predykcji dla \(y_{new}}):
(\hat{y}_h \pm t_{(1-alfa/2, n-2)} \times \sqrt{MSE \times \left( 1+dfrac{1}{n} + \dfrac{(x_h- \bar{x})^2}{ \sum(x_i- \bar{x})^2}right)})
Aby zobaczyć, jak to się ma do wzoru na przedział ufności dla \u}{Y}:
(\hat{y}_h \pm t_{(1-alfa/2, n-2)} \times \sqrt{MSE \left(\dfrac{1}{n} + dfrac{(x_h-bar{x})^2}{sum(x_i-bar{x})^2}right)})
Zauważmy, że jedyną różnicą we wzorach jest to, że błąd standardowy predykcji dla y_{new}} ma w sobie dodatkowy człon MSE, którego nie ma błąd standardowy dopasowania dla y_{Y}}.
Postarajmy się zrozumieć przedział predykcji, aby zobaczyć, co powoduje dodatkowy termin MSE. Aby to zrobić, zacznijmy najpierw od łatwiejszego problemu. Zastanów się, jak moglibyśmy przewidzieć nową odpowiedź \(y_{new}} w konkretnym \(x_{h}}), gdyby średnia odpowiedzi \(\mu_{Y}} w \(x_{h}}) była znana. To znaczy, załóżmy, że wiadomo, że średnia śmiertelność z powodu raka skóry przy x_{h} = 40^{o} N wynosi 150 zgonów na milion (z wariancją 400)? Jaka jest przewidywana śmiertelność z powodu raka skóry w Columbus, Ohio?
Ponieważ \u_{Y} = 150 \) i \u_{sigma^{2} = 400 \) są znane, możemy skorzystać z „reguły empirycznej”, która mówi między innymi, że 95% pomiarów danych o rozkładzie normalnym mieści się w granicach 2 odchyleń standardowych od średniej. Oznacza to, że 95% pomiarów mieści się w przedziale pomiędzy:
(∗- 2 odchylenia standardowe) i ∗(∗+ 2 odchylenia standardowe).
Zastosowanie reguły 95% do naszego przykładu z \u_mu_{Y} = 150\u_ i \u_sigma= 20\u_u_u_y}:
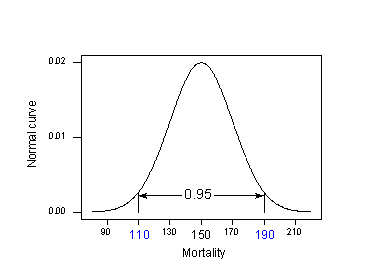
95% współczynników umieralności na raka skóry w lokalizacjach na 40 stopniu szerokości geograficznej północnej znajduje się w przedziale przedziału przedzielonym przez:
150 – 2(20) = 110 i 150 + 2(20) = 190.
To znaczy, jeśli ktoś chciałby znać współczynnik umieralności na raka skóry dla lokalizacji na 40 stopniu szerokości geograficznej północnej, naszym najlepszym przypuszczeniem byłoby gdzieś pomiędzy 110 a 190 zgonów na 10 milionów. Problem polega na tym, że w naszych obliczeniach wykorzystaliśmy \(\mu_{Y}} i \(\sigma}), wartości populacji, których zazwyczaj nie znamy. Rzeczywistość wkracza:
- Średnia \(\mu_{Y}) zwykle nie jest znana. Logiczną rzeczą do zrobienia jest oszacowanie go za pomocą przewidywanej odpowiedzi \(\hat{y}}. Kosztem użycia \u_that{y}} do oszacowania \u_mu_{y} jest wariancja \u_that{y}. Oznacza to, że różne próbki dałyby różne przewidywania, więc musimy wziąć pod uwagę wariancję \(\hat{y}}.
- Wariancja \(\sigma^{2}}zwykle nie jest znana. Logiczną rzeczą do zrobienia jest oszacowanie jej za pomocą MSE.
Ponieważ musimy oszacować te nieznane wielkości, wariacja w przewidywaniu nowej odpowiedzi zależy od dwóch składników:
- Wariacja spowodowana oszacowaniem średniej \(\mu{Y}}) z \(\hat{y}_h\) , którą oznaczamy „\(\sigma^2(\hat{Y}_h)\).”(Zwróć uwagę, że oszacowanie tej wielkości jest po prostu kwadratem standardowego błędu dopasowania, który pojawia się we wzorze na przedział ufności.)
- zmienność odpowiedzi y, którą oznaczamy jako „\(\sigma^2\).”(Zauważ, że wielkość ta jest szacowana, jak zwykle, za pomocą błędu średniokwadratowego MSE.)
Dodając dwie składowe wariancji, otrzymujemy:
(\sigma^2+ \sigma^2(\hat{Y}_h)\)
którą szacujemy przez:
(MSE+MSE \left( \dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \right) =MSEleft( 1+ \dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2}
Czy rozpoznajesz tę wielkość? To po prostu wariancja predykcji, która pojawia się we wzorze na przedział predykcji \(y_{new}\)!
Porównajmy te dwa przedziały jeszcze raz:
Przedział ufności dla \(\mu_{Y}}colon \hat{y}_h \pm t_{(1-alfa/2, n-2)} \times \sqrt{MSE \times \left( \frac{1}{n} + \frac{(x_h-bar{x})^2}{ \sum(x_i-bar{x})^2}right)})
Przedział predykcji dla \(y_{new}colon \hat{y}_h \pm t_{(1-alfa/2, n-2)} \times \sqrt{MSE \left( 1+frac{1}{n} + \frac{(x_h-bar{x})^2}{ suma(x_i-bar{x})^2}prawa)})
Jakie są praktyczne implikacje różnicy w tych dwóch wzorach?
- Ponieważ przedział predykcji ma dodatkowy składnik MSE, przedział ufności dla ∗mu_{Y}} w punkcie x_{h}} zawsze będzie węższy niż odpowiadający mu przedział predykcji dla ∗mu_{y}} w punkcie x_{h}}.
- Obliczając przedział przy średniej z próby wartości predyktorów \(\left(x_{h} = \bar{x}}right)\) i zwiększając liczebność próby n, błąd standardowy przedziału ufności może zbliżyć się do 0. Ponieważ przedział predykcji ma dodatkowy człon MSE, błąd standardowy przedziału predykcji nie może zbliżyć się do 0.
Pierwszą implikację najłatwiej dostrzec studiując poniższy wykres dla naszego przykładu śmiertelności z powodu raka skóry:
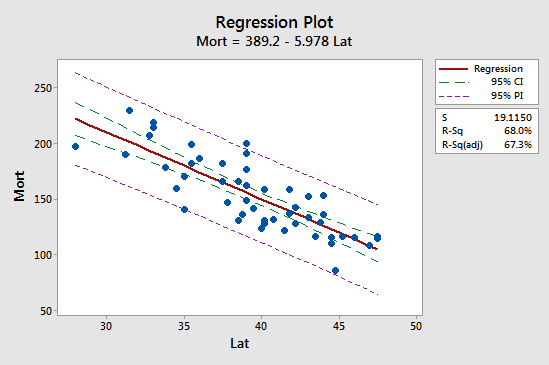
Zauważ, że przedział predykcji (95% PI, w kolorze fioletowym) jest zawsze szerszy niż przedział ufności (95% CI, w kolorze zielonym). Ponadto, oba przedziały są najwęższe przy średniej wartości predyktorów (około 39,5).