W tym rozdziale dowiemy się, jak znaleźć pierwiastek(i) równania czworokątnego. Korzenie są również nazywane punktami przecięcia x lub zerami. Funkcja kwadratowa jest przedstawiana graficznie jako parabola z wierzchołkiem znajdującym się w punkcie początkowym, poniżej osi x lub powyżej osi x. W związku z tym funkcja kwadratowa może mieć jeden, dwa lub zero korzeni.
Kiedy jesteśmy proszeni o rozwiązanie równania kwadratowego, tak naprawdę jesteśmy proszeni o znalezienie korzeni. Widzieliśmy już, że dopełnianie do kwadratu jest użyteczną metodą rozwiązywania równań kwadratowych. Metoda ta może być użyta do wyprowadzenia wzoru na kwadrat, który jest używany do rozwiązywania równań kwadratowych. W rzeczywistości, korzenie funkcji,
f (x) = ax2 + bx + c
są określone przez wzór na kwadrat. Korzenie funkcji są punktami przecięcia x. Z definicji, współrzędna y punktów leżących na osi x jest równa zero. Dlatego, aby znaleźć korzenie funkcji kwadratowej, ustawiamy f (x) = 0 i rozwiązujemy równanie,
ax2 + bx + c = 0.
We can do this by completing the square as,
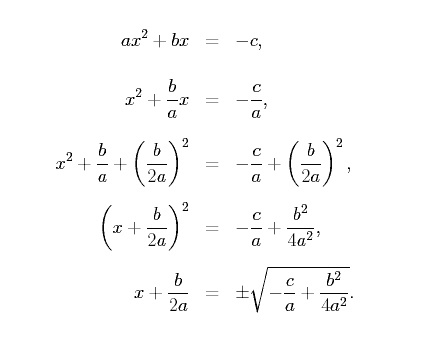
Solving for x and simplifying we have,
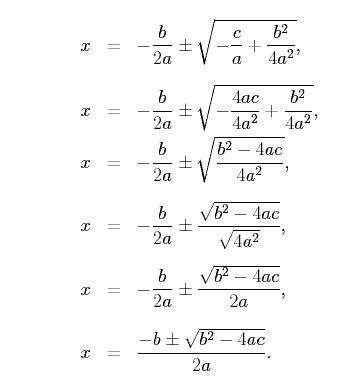
Thus, the roots of a quadratic function are given by,
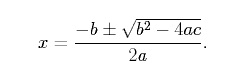
This formula is called the quadratic formula, and its derivation is included so that you can see where it comes from. We call the term b2 −4ac the discriminant. The discriminant is important because it tells you how many roots a quadratic function has. Specifically, if
1. b2 −4ac < 0 There are no real roots.
2. b2 −4ac = 0 There is one real root.
3. b2 −4ac > 0 There are two real roots.
We will examine each case individually.
Przypadek 1: Brak pierwiastków rzeczywistych
Jeśli wyróżnik funkcji kwadratowej jest mniejszy od zera, to funkcja ta nie ma pierwiastków rzeczywistych, a parabola, którą reprezentuje, nie przecina osi x. Ponieważ wzór na funkcję kwadratową wymaga wzięcia pierwiastka kwadratowego z wyróżnika, ujemny wyróżnik stwarza problem, ponieważ pierwiastek kwadratowy liczby ujemnej nie jest określony na linii rzeczywistej. Przykładem funkcji kwadratowej bez pierwiastków rzeczywistych jest funkcja,
f(x) = x2 – 3x + 4.
Zauważmy, że wyróżnik funkcji f(x) jest ujemny,
b2 -4ac = (-3)2- 4 – 1 – 4 = 9 – 16 = -7.
Funkcję tę można przedstawić graficznie w postaci paraboli otwierającej się ku górze, której wierzchołek leży powyżej osi x. Zatem wykres nigdy nie przecina osi x i nie ma korzeni, jak pokazano poniżej,
Przypadek 2: Jeden pierwiastek rzeczywisty
Jeśli wyróżnik funkcji kwadratowej jest równy zero, to funkcja ta ma dokładnie jeden pierwiastek rzeczywisty i przecina oś x w jednym punkcie. Aby się o tym przekonać, we wzorze na funkcję kwadratową ustawiamy b2 -4ac = 0, aby otrzymać,
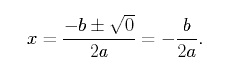
Zauważ, że 
jest współrzędną x wierzchołka paraboli. Zatem parabola ma dokładnie jeden pierwiastek rzeczywisty, gdy wierzchołek paraboli leży dokładnie na osi x. Najprostszym przykładem funkcji kwadratowej, która ma tylko jeden pierwiastek rzeczywisty, jest funkcja,
y = x2,
gdzie pierwiastkiem rzeczywistym jest x = 0.
Innym przykładem funkcji kwadratowej z jednym pierwiastkiem rzeczywistym jest funkcja,
f(x) = -4×2 + 12x – 9.
Zauważmy, że wyróżnik funkcji f(x) wynosi zero,
b2 -4ac = (12)2- 4 – -4 -9 = 144 – 144 = 0.
Funkcję tę przedstawia graficznie parabola, która otwiera się w dół i ma wierzchołek (3/2, 0), leżący na osi x. Thus, the graph intersects the x-axis at exactly one point (i.e. has one root) as shown below,
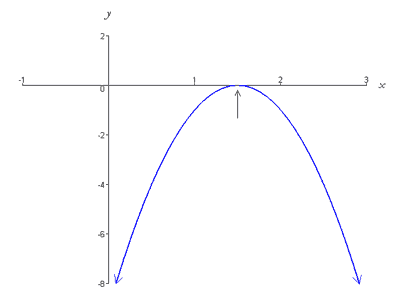
Case 3: Two Real Roots
If the discriminant of a quadratic function is greater than zero, that function has two real roots (x-intercepts). Taking the square root of a positive real number is well defined, and the two roots are given by,
An example of a quadratic function with two real roots is given by,
f(x) = 2×2− 11x + 5.
Notice that the discriminant of f(x) is greater than zero,