Funkcja Produkcji Cobba-Douglasa modeluje zależność pomiędzy wynikiem produkcji a nakładami produkcyjnymi (czynnikami). Jest ona wykorzystywana do obliczania stosunku nakładów do siebie dla efektywnej produkcji oraz do szacowania zmian technologicznych w metodach produkcji. Ogólna postać funkcji produkcji Cobba-Douglasa dla zbioru ∗ nakładów jest taka, że ∗ oznacza wielkość produkcji, ∗ x_{i}} oznacza nakład, a ∗ gamma i ∗ alfa są parametrami określającymi ogólną efektywność produkcji i reaktywność produkcji na zmiany wielkości nakładów. Zastosowanie tej formy funkcyjnej do pomiaru produkcji zawdzięczamy matematykowi Charlesowi Cobbowi i ekonomiście Paulowi Douglasowi, którzy wykorzystali ją do rozważenia względnego znaczenia dwóch czynników produkcji, pracy i kapitału, w produkcji przemysłowej w USA w latach 1899-1922. W swoim oryginalnym modelu Cobb i Douglas ograniczyli parametry elastyczności produkcji \(\alfa_{1}} i \(\alfa_{2}} do przedziału \(\alfa_{i}}lewa(0,1,1,1)\) i do sumy jeden, co oznacza stałe korzyści skali. Funkcja ta ma postać, gdzie \(x_{1}} i \(x_{2}}) oznaczają odpowiednio pracę i kapitał. Przyjmując logarytm naturalny z obu stron równania, dla danych dotyczących produkcji, pracy i kapitału można oszacować parametry ∗(∗gamma) i ∗alpha_{1}} przy użyciu metody Ordinary Least Squares. W oparciu o swoje dane, Cobb i Douglas ustalili wartość 0,75 dla parametru \(\alpha_{1}}, co oznacza, że praca stanowiła trzy czwarte wartości produkcji przemysłowej w USA (kapitał stanowił pozostałą jedną czwartą) w badanym okresie. Ich szacunek dla parametru efektywności wynosi 1,01, który, ponieważ jest większy niż 1, odzwierciedla pozytywny wpływ nieobserwowalnych sił na produkcję poprzez kombinację pracy i kapitału.
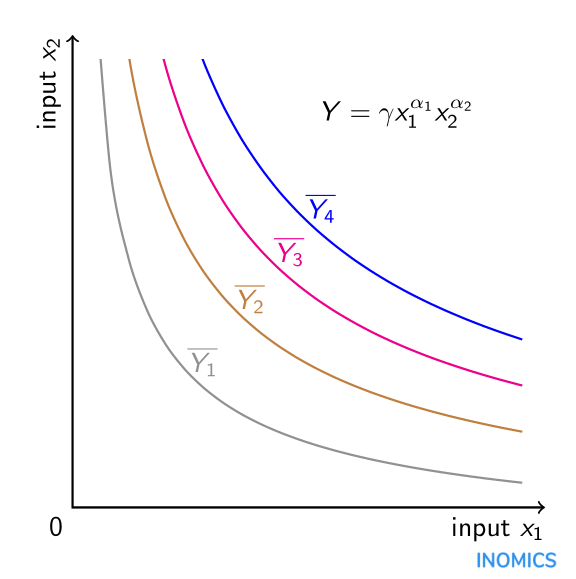
Multiplikatywny charakter funkcji produkcji Cobba-Douglasa, zakładając dodatnie wartości dla \u00_{i}, oznacza, że czynniki produkcji są komplementarne w produkcji. W standardowym modelu pracy i kapitału, zwiększenie ilości kapitału zwiększa produkcję nie tylko bezpośrednio, ale również pośrednio poprzez wpływ na wydajność pracy. Z matematycznego punktu widzenia pochodna przekrojowa produkcji \(Y) względem pracy \(x_{1}} i kapitału \(x_{2}} jest dodatnia. Po prostu dodanie do procesu produkcji albo więcej pracy, albo więcej kapitału (ale nie obu) zwiększa produkcję, choć w malejącym tempie. Ponadto, elastyczność substytucji pomiędzy nakładami jest stała i równa jeden ze względu na formę funkcjonalną. Dwuskładnikową funkcję produkcji Cobba-Douglasa można przedstawić graficznie w postaci izokwant: kombinacji obu nakładów, dla których produkcja jest stała. Na przedstawionym wykresie występują cztery takie izokwanty dla (stałych) poziomów produkcji: \(\overline{Y_{1}}), \(\overline{Y_{2}}), \(\overline{Y_{3}}) i \(\overline{Y_{4}}). Im dalej izokwanta od początku, tym większy poziom produkcji \(\overline{Y_{4}}> \overline{Y_{3}}> \overline{Y_{2}}> \overline{Y_{1}}). To, która dokładnie kombinacja nakładów ®(x_{1}} i ®(x_{2}}) jest optymalna dla produkcji, zależy od budżetu, jakim dysponuje producent, a także od stosunku kosztów nakładów ®(x_{2}}) do nakładów ®(x_{1}}), który można uwzględnić na wykresie w postaci linii izokosztów (zob. artykuł o elastyczności substytucji).
Cobb i Douglas sami przyznali, że ich funkcja produkcji nie opiera się na solidnych podstawach teoretycznych, ani nie powinna być rozumiana jako prawo produkcji; stanowi ona jedynie statystyczne przybliżenie zaobserwowanych relacji między nakładami produkcyjnymi a produkcją. Niemniej jednak, jej proste matematyczne właściwości są atrakcyjne dla ekonomistów i doprowadziły do tego, że stała się standardem w teorii mikroekonomicznej w ciągu ostatniego stulecia.
Dalsza lektura:
Aby poznać tło i przegląd głównych właściwości funkcji produkcji Cobba-Douglasa, zobacz w szczególności sekcje 6, 7 i 8 oryginalnego artykułu Cobba i Douglasa, „A Theory of Production” (The American Economic Review, 1928). Wartości ˆ(x_{i}} reprezentują pozycje konsumpcyjne, a kiedy funkcja użyteczności jest maksymalizowana z zastrzeżeniem ograniczenia budżetowego, wartości ˆ(alfa_{i}}) wskazują, jak dana osoba optymalnie rozdzieli budżet pomiędzy pozycje.