Rzuty
Po opisaniu pojęcia redukcji wymiaru oraz niektórych zastosowań SVD i analizy składowych głównych, skupimy się na szczegółach związanych z matematyką stojącą za tymi pojęciami. Zaczniemy od projekcji. Rzutowanie jest pojęciem algebry liniowej, które pomaga nam zrozumieć wiele operacji matematycznych, które wykonujemy na danych wielowymiarowych. Aby uzyskać więcej szczegółów, możesz przejrzeć projekty w książce o algebrze liniowej. Tutaj przedstawiamy szybki przegląd, a następnie podajemy kilka przykładów związanych z analizą danych.
Jako przegląd, pamiętaj, że projekcje minimalizują odległość między punktami i podprzestrzenią.

Na rysunku powyżej punkt na górze wskazuje na punkt w przestrzeni. W tym konkretnym komiksie przestrzeń jest dwuwymiarowa, ale my powinniśmy myśleć abstrakcyjnie. Przestrzeń jest reprezentowana przez płaszczyznę kartezjańską, a linia, na której stoi mały człowiek, jest podprzestrzenią punktów. Rzut na tę podprzestrzeń jest miejscem, które jest najbliżej pierwotnego punktu. Geometria mówi nam, że możemy znaleźć ten najbliższy punkt, spuszczając prostą prostopadłą (linia przerywana) z punktu do przestrzeni. Mała osóbka stoi na rzucie. Odległość, jaką ta osoba musiała przebyć od początku do nowego rzutowanego punktu, nazywamy współrzędną.
Do wyjaśnienia rzutów będziemy używać standardowej notacji algebry macierzy dla punktów: jest punktem w -wymiarowej przestrzeni i jest mniejszą podprzestrzenią.
Prostszy przykład z N=2
Jeśli pozwolimy . Możemy to wykreślić w ten sposób:
mypar (1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)text(2,3," Y",pos=4,cex=3)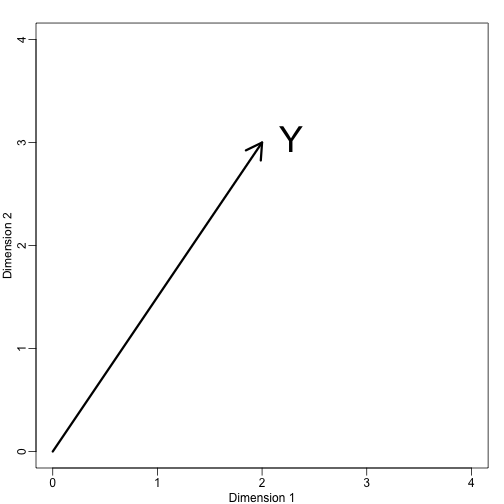
Możemy od razu zdefiniować układ współrzędnych rzutując ten wektor na przestrzeń określoną przez: (oś x) i (oś y). Rzuty na podprzestrzeń zdefiniowaną przez te punkty wynoszą odpowiednio 2 i 3:
Mówimy, że i to współrzędne, a to bazy.
Zdefiniujmy teraz nową podprzestrzeń. Czerwona linia na poniższym wykresie jest podzbiorem zdefiniowanym przez punkty spełniające z . Musimy więc znaleźć punkt, który minimalizuje odległość między i . W algebrze liniowej uczymy się, że różnica między tymi punktami jest ortogonalna do przestrzeni, więc:
to implikuje, że:
i:
Tutaj kropka reprezentuje iloczyn punktowy: .
Następujący kod R potwierdza, że to równanie działa:
mypar(1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)abline(0,0.5,col="red",lwd=3) #if x=2c and y=c then slope is 0.5 (y=0.5x)text(2,3," Y",pos=4,cex=3)y=c(2,3)x=c(2,1)cc = crossprod(x,y)/crossprod(x)segments(x*cc,x*cc,y,y,lty=2)text(x*cc,x*cc,expression(hat(Y)),pos=4,cex=3)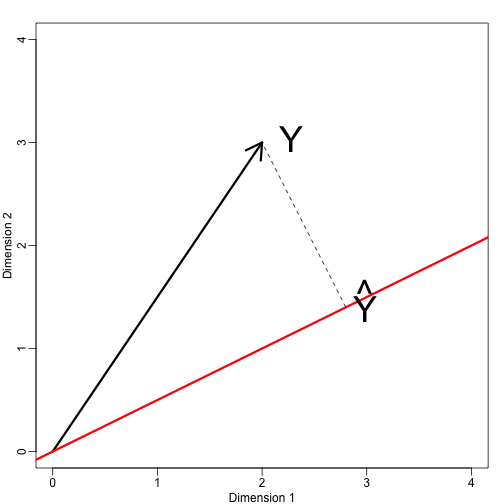
Zauważmy, że jeśli było takie, że , to jest proste i przestrzeń się nie zmienia. To uproszczenie jest jednym z powodów, dla których lubimy macierze ortogonalne.
Przykład: Średnia z próby jest rzutem
Pozwólmy i jest przestrzenią rozpiętą przez:
W tej przestrzeni wszystkie składowe wektorów mają tę samą liczbę, więc możemy myśleć o tej przestrzeni jako reprezentującej stałe: w rzucie każdy wymiar będzie miał tę samą wartość. Więc co minimalizuje odległość między i ?
Gdy mówimy o problemach takich jak ten, czasami używamy dwuwymiarowych figur, takich jak ta powyżej. Po prostu abstrahujemy i myślimy o punkcie w i jako o podprzestrzeni zdefiniowanej przez mniejszą liczbę wartości, w tym przypadku tylko jedną: .
Powracając do naszego pytania, wiemy, że projekcja to:
która w tym przypadku jest średnią:
Tutaj również równie łatwo byłoby użyć rachunku:
Przykład: Regresja to też rzut
Podajmy nieco bardziej skomplikowany przykład. Prostą regresję liniową można również wyjaśnić za pomocą projekcji. Nasze dane (nie będziemy już używać tej notacji) to znów wektor, a nasz model przewiduje za pomocą linii . We want to find the and that minimize the distance between and the space defined by:
with:
Our matrix is and any point in can be written as .
The equation for the multidimensional version of orthogonal projection is:
which we have seen before and gives us:
And the projection to is therefore: