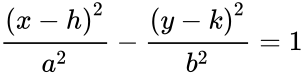Semi-major axis | Space Wiki | Organic Articles

File:Semimajoraxis.png

Oś półmajora elipsy

W geometrii termin oś półmajora (także oś semimajora) jest używany do opisu wymiarów elips i hiperboli.

Elipsa
Hyperbola
Astronomy
Orbital period
Średnia odległość
Energia; obliczanie osi półmajora z wektorów stanu
Przykład

Elipsa

Osią główną elipsy jest jej najdłuższa średnica, linia, która przebiega przez środek i oba ogniska, a jej końce znajdują się w najszerszych punktach kształtu. Oś półmagoryczna jest połową osi głównej, a więc biegnie od środka, przez ognisko i do brzegu elipsy.

Jest ona związana z osią półmagoryczną ${displaystyle b,}$ poprzez mimośród ${displaystyle e,}}$ i odbytnicę półpłaską ${displaystyle ell \\!}$ , w następujący sposób:

${displaystyle b=a{sqrt {1-e^{2}}}}}$ ${displaystyle ell =a(1-e^{2})\\}$ ${displaystyle a ell =b^{2})\\,\!}$ .

Parabolę można otrzymać jako granicę ciągu elips, w których jedno ognisko jest utrzymywane w stałym położeniu, podczas gdy drugiemu pozwala się przesuwać dowolnie daleko w jednym kierunku, zachowując ${displaystyle ^{2}},^!}$ stałą. Zatem ${displaystyle a,}$ i ${displaystyle b,}$ dążą do nieskończoności, ${displaystyle a,}}$ szybciej niż ${displaystyle b}$ .

Oś półmajora to średnia wartość najmniejszej i największej odległości od jednego ogniska do punktów na elipsie. Rozważmy teraz to równanie we współrzędnych biegunowych, z jednym ogniskiem na początku, a drugim na dodatniej osi x,

${displaystyle r(1-e=cos ™theta )=l,™!}$

The mean value of $r={\ell \over {1+e}}\,\!$ and $r={\ell \over {1-e}}\,\!$ , is $a={\ell \over {1-e^{2}}}\,\!$ .

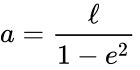
Hyperbola

The semi-major axis of a hyperbola is one half of the distance between the two branches; if this is a in the x-direction the equation is:

${\frac {\left(x-h\right)^{2}}{a^{2}}}-{\frac {\left(y-k\right)^{2}}{b^{2}}}=1$

In terms of the semi-latus rectum and the eccentricity we have

$a={\ell \over e^{2}-1}$

Astronomy

Orbital period

In astrodynamics the orbital period $T\,$ of a small body orbiting a central body in a circular or elliptical orbit is:

$T=2\pi {\sqrt {a^{3}/\mu }}$

where:

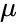
${displaystyle a$ jest długością osi półmajora orbity ${displaystyle \u}$ jest standardowym parametrem grawitacyjnym

Zauważmy, że dla wszystkich elips o danej osi półmajora okres orbitalny jest taki sam, niezależnie od mimośrodu.

W astronomii, oś półmajora jest jednym z najważniejszych elementów orbitalnych orbity, obok okresu orbitalnego. Dla obiektów Układu Słonecznego, oś półmajora jest związana z okresem orbity trzecim prawem Keplera (pierwotnie wyprowadzonym empirycznie),

${displaystyle T^{2}}=a^{3}}},}$

gdzie T jest okresem w latach, a a jest osią półmajora w jednostkach astronomicznych. Ta postać okazuje się być uproszczeniem ogólnej postaci dla problemu dwóch ciał, wyznaczonej przez Newtona:

${displaystyle T^{2}={}frac {4}pi ^{2}}{G(M+m)}}a^{3}}}},}$

gdzie G jest stałą grawitacyjną, a M jest masą ciała centralnego, a m masą ciała orbitującego. Zazwyczaj masa ciała centralnego jest o tyle większa od masy ciała orbitującego, że m można zignorować. Przyjmując to założenie i używając typowych jednostek astronomicznych otrzymujemy prostszą formę, którą odkrył Kepler.

Co ciekawe, ścieżka ciała krążącego wokół barycentrum i jego ścieżka względem ciała pierwotnego są elipsami. Stosowana w astronomii oś półmajora jest zawsze odległością między pierwotną a wtórną, dlatego parametry orbit planet podawane są w ujęciu heliocentrycznym. Różnicę pomiędzy orbitą primocentryczną a orbitą „absolutną” najlepiej zilustrować na przykładzie układu Ziemia-Księżyc. Stosunek mas w tym przypadku wynosi 81,30059. Odległość charakterystyczna Ziemia-Księżyc, oś półmajora geocentrycznej orbity księżycowej, wynosi 384 400 km. Natomiast księżycowa orbita barycentryczna ma oś półmajora 379 700 km, przy czym przeciw-orbita Ziemi zajmuje różnicę 4 700 km. Średnia barycentryczna prędkość orbitalna Księżyca wynosi 1,010 km/s, podczas gdy prędkość Ziemi 0,012 km/s. Suma tych prędkości daje geocentryczną średnią prędkość orbitalną Księżyca, 1.022 km/s; tę samą wartość można uzyskać rozważając tylko wartość geocentrycznej osi półmajora.

Średnia odległość

Często mówi się, że oś półmajora jest „średnią” odległością pomiędzy głównym (ogniskiem elipsy) a orbitującym ciałem. Nie jest to całkiem dokładne, ponieważ zależy to od tego, nad czym ta średnia jest brana.

uśredniając odległość nad anomalią mimośrodową (q.v.) rzeczywiście otrzymujemy oś półmajora.
obliczanie odległości przez prawdziwą anomalię (prawdziwy kąt orbitalny, mierzony w ognisku) daje, co dziwne, oś półmajora ${displaystyle b=a{sqrt {1-e^{2}}}}},\!$
przekroczenie średniej anomalii (ułamek okresu orbitalnego, który upłynął od perycentrum, wyrażony jako kąt), w końcu daje średnią czasową (co jest tym, co „średnia” zwykle oznacza dla laika): ${displaystyle a(1+{frac {e^{2}}{2}})}$ .

Średnia czasowa odwrotności promienia, ${displaystyle r^{-1}},^!}$ , wynosi ${displaystyle a^{-1},^!}$ .

Energia; obliczanie osi półmajora z wektorów stanu

W astrodynamice oś półmajora ${displaystyle a,}$ można obliczyć z wektorów stanu orbitalnego:

$a={-\mu \over {2\epsilon }}\,$ for an elliptical orbit and $a={\mu \over {2\epsilon }}\,$ for a hyperbolic trajectory

and

$\epsilon ={v^{2} \over {2}}-{\mu \over \left|\mathbf {r} \right|}$ (specific orbital energy)

and

$\mu =GM\,$ (standard gravitational parameter),

where:

$v\,$ is orbital velocity from velocity vector of an orbiting object,
$\mathbf {r} \,$ is cartesian position vector of an orbiting object in coordinates of a reference frame with respect to which the elements of the orbit are to be calculated (e.g. geocentryczna równikowa dla orbity wokół Ziemi, lub heliocentryczna ekliptyczna dla orbity wokół Słońca),
${displaystyle G,}$ jest stałą grawitacyjną,
${displaystyle M,}$ masa ciała centralnego.

Zauważmy, że dla danego ciała centralnego i całkowitej energii właściwej, oś półmajora jest zawsze taka sama, niezależnie od mimośrodu. I odwrotnie, dla danego ciała centralnego i osi półmajora, całkowita energia właściwa jest zawsze taka sama.

Przykład

Międzynarodowa Stacja Kosmiczna ma okres orbitalny 91,74 minuty, stąd oś półmajora wynosi 6738 km . Każda minuta więcej odpowiada ok. 50 km więcej: dodatkowe 300 km długości orbity zajmuje 40 sekund, mniejsza prędkość to dodatkowe 20 sekund.