Magiczne Kwadraty są kwadratowymi siatkami ze specjalnym układem liczb w nich. Liczby te są specjalne, ponieważ każdy rząd, kolumna i przekątna dodaje się do tej samej liczby. Więc dla przykładu poniżej, 15 jest magiczną liczbą. Czy możesz to obliczyć, wiedząc, że w kwadracie użyto liczb od 1 do 9?

Również dwie liczby, które znajdują się naprzeciwko siebie po drugiej stronie środkowej liczby, będą sumować się do tej samej liczby. Tak więc w powyższym kwadracie, 8 + 2 = 10 , 6 + 4 = 10, 1 + 9 = 10 i 3 + 7 = 10. Dlaczego tak jest?
„Zamówienie” magicznego kwadratu mówi, ile rzędów lub kolumn ma. Więc kwadrat z 3 rzędami i kolumnami jest Order 3, a kwadrat z 4 rzędami i kolumnami jest Order 4 i tak dalej. Jeśli chcesz dowiedzieć się więcej o tym, jak tworzyć własne magiczne kwadraty, i matematyki za tym wszystkim, można przejść do niektórych innych stron na stronie internetowej, takich jak Magiczne kwadraty i Magiczne kwadraty II .
Ale dlaczego są one nazywane magiczne?
Więc numery w Magicznym Kwadracie są specjalne, ale dlaczego są one nazywane magiczne? Wydaje się, że od najdawniejszych czasów były one związane ze światem nadprzyrodzonym i magicznym. Najwcześniejszy zapis o magicznych kwadratach pochodzi z Chin z ok. 2200 r. p.n.e. i nosi nazwę „Lo-Shu”. Istnieje legenda, która mówi, że cesarz Yu zobaczył ten magiczny kwadrat na grzbiecie boskiego żółwia w Żółtej Rzece.
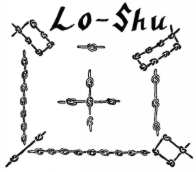
Czarne węzły pokazują liczby parzyste, a białe nieparzyste. Przyjrzyj się uważnie, a zobaczysz, że ten starożytny kwadrat magiczny jest taki sam jak nasz przykład powyżej. Kwadraty magiczne zostały po raz pierwszy wspomniane w świecie zachodnim w dziele Theona ze Smyrny. Były one również używane przez arabskich astrologów w IX wieku, aby pomóc w opracowaniu horoskopów. Praca greckiego matematyka Moschopoulosa w 1300 r. przyczyniła się do rozpowszechnienia wiedzy o kwadratach magicznych. Tak więc jesteśmy tu teraz, ponad 700 lat później, a nauczyciele używają ich w klasie do rozwiązywania problemów i ćwiczenia dodawania.
Możesz zrobić podobne kwadraty magiczne, rzędu 3, używając różnych liczb. Czy widzisz jakieś wzory w liczbach, które działają?