Projektionen
Nachdem wir nun das Konzept der Dimensionsreduktion und einige Anwendungen der SVD und der Hauptkomponentenanalyse beschrieben haben, wollen wir uns nun den mathematischen Details widmen, die sich dahinter verbergen. Wir beginnen mit Projektionen. Eine Projektion ist ein Konzept der linearen Algebra, das uns hilft, viele der mathematischen Operationen zu verstehen, die wir mit hochdimensionalen Daten durchführen. Für weitere Einzelheiten können Sie Projekte in einem Buch über lineare Algebra nachlesen. Hier geben wir einen kurzen Überblick und zeigen dann einige Beispiele zur Datenanalyse.
Zur Erinnerung: Projektionen minimieren den Abstand zwischen Punkten und Unterräumen.

In der Abbildung oben zeigt der Punkt oben auf einen Punkt im Raum. In dieser speziellen Karikatur ist der Raum zweidimensional, aber wir sollten abstrakt denken. Der Raum wird durch die kartesische Ebene dargestellt, und die Linie, auf der die kleine Person steht, ist ein Unterraum von Punkten. Die Projektion auf diesen Unterraum ist der Ort, der dem ursprünglichen Punkt am nächsten ist. Die Geometrie sagt uns, dass wir diesen nächstgelegenen Punkt finden können, indem wir eine senkrechte Linie (gestrichelte Linie) von dem Punkt in den Raum fällen. Die kleine Person steht auf der Projektion. Die Strecke, die diese Person vom Ursprung bis zum neuen projizierten Punkt zurücklegen musste, wird als Koordinate bezeichnet.
Für die Erklärung von Projektionen werden wir die Standard-Matrixalgebra-Notation für Punkte verwenden: ist ein Punkt im -dimensionalen Raum und ist kleiner Unterraum.
Einfaches Beispiel mit N=2
Wenn wir . Wir können es so darstellen:
mypar (1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)text(2,3," Y",pos=4,cex=3)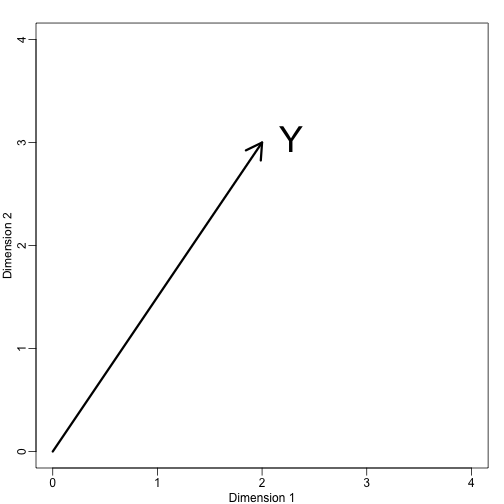
Wir können sofort ein Koordinatensystem definieren, indem wir diesen Vektor auf den Raum projizieren, der durch: (die x-Achse) und (die y-Achse). Die Projektionen von auf den durch diese Punkte definierten Unterraum sind 2 bzw. 3:
Wir sagen, dass und die Koordinaten sind und dass die Basen sind.
Nun definieren wir einen neuen Unterraum. Die rote Linie in der Grafik unten ist die Untermenge, die durch Punkte definiert ist, die mit erfüllt sind. Die Projektion von onto ist der nächstgelegene Punkt auf . Wir müssen also den Punkt finden, der den Abstand zwischen und minimiert. In der linearen Algebra lernen wir, dass die Differenz zwischen diesen Punkten orthogonal zum Raum ist, also:
Das impliziert, dass:
und:
Hier steht der Punkt für das Punktprodukt: .
Der folgende R-Code bestätigt, dass diese Gleichung funktioniert:
mypar(1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)abline(0,0.5,col="red",lwd=3) #if x=2c and y=c then slope is 0.5 (y=0.5x)text(2,3," Y",pos=4,cex=3)y=c(2,3)x=c(2,1)cc = crossprod(x,y)/crossprod(x)segments(x*cc,x*cc,y,y,lty=2)text(x*cc,x*cc,expression(hat(Y)),pos=4,cex=3)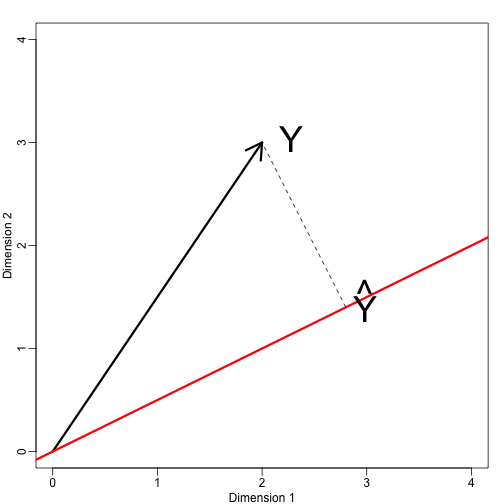
Beachten Sie, dass wenn so war, dass , dann ist einfach und der Raum ändert sich nicht. Diese Vereinfachung ist ein Grund, warum wir orthogonale Matrizen mögen.
Beispiel: Der Stichprobenmittelwert ist eine Projektion
Lassen wir und den Raum, der aufgespannt wird durch:
In diesem Raum sind alle Komponenten der Vektoren die gleiche Zahl, so dass wir uns diesen Raum als Darstellung der Konstanten vorstellen können: in der Projektion hat jede Dimension den gleichen Wert. Was also minimiert den Abstand zwischen und?
Wenn wir über Probleme wie dieses sprechen, verwenden wir manchmal zweidimensionale Figuren wie die oben abgebildete. Wir abstrahieren einfach und stellen uns einen Punkt in und als Unterraum vor, der durch eine geringere Anzahl von Werten definiert ist, in diesem Fall nur durch einen: .
Zurück zu unserer Frage wissen wir, dass die Projektion ist:
Was in diesem Fall der Durchschnitt ist:
Hier wäre es auch genauso einfach gewesen, die Infinitesimalrechnung zu benutzen:
Beispiel: Regression ist auch eine Projektion
Lassen Sie uns ein etwas komplizierteres Beispiel geben. Die einfache lineare Regression kann auch mit Projektionen erklärt werden. Unsere Daten (wir werden die Schreibweise nicht mehr verwenden) sind wieder ein Vektor und unser Modell sagt mit einer Linie voraus. We want to find the and that minimize the distance between and the space defined by:
with:
Our matrix is and any point in can be written as .
The equation for the multidimensional version of orthogonal projection is:
which we have seen before and gives us:
And the projection to is therefore: