În discuția noastră despre intervalul de încredere pentru \(\mu_{Y}\), am folosit formula pentru a investiga ce factori afectează lățimea intervalului de încredere. Nu este nevoie să o facem din nou. Deoarece formulele sunt atât de asemănătoare, se pare că factorii care afectează lățimea intervalului de predicție sunt identici cu factorii care afectează lățimea intervalului de încredere.
Să investigăm în schimb formula pentru intervalul de predicție pentru \(y_{new}\):
\(\hat{y}_h \pm t_{{(1-\alpha/2, n-2)} \times \sqrt{MSE \times \left( 1+\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\})
pentru a vedea cum se compară cu formula pentru intervalul de încredere pentru \(\mu_{Y}\):
(\hat{y}_h \pm t_{(1-\alpha/2, n-2)} \times \sqrt{MSE \left(\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\dreapta)}\)
Observați că singura diferență în formule este că eroarea standard a predicției pentru \(y_{new}\) are un termen MSE suplimentar în ea, pe când eroarea standard a ajustării pentru \(\mu_{Y}\) nu are.
Să încercăm să înțelegem intervalul de predicție pentru a vedea care este cauza termenului MSE suplimentar. În acest sens, să începem mai întâi cu o problemă mai ușoară. Gândiți-vă cum am putea prezice un nou răspuns \(y_{new}\) la un anumit \(x_{h}\) dacă media răspunsurilor \(\mu_{Y}\) la \(x_{h}\) ar fi cunoscută. Adică, să presupunem că se știe că media mortalității prin cancer de piele la \(x_{h} = 40^{o}\) N este de 150 decese la un milion (cu o varianță de 400)? Care este mortalitatea prognozată a cancerului de piele în Columbus, Ohio?
Pentru că \(\mu_{Y} = 150 \) și \( \sigma^{2} = 400\) sunt cunoscute, putem profita de „regula empirică”, care afirmă, printre altele, că 95% din măsurătorile datelor distribuite normal se află în limitele a 2 deviații standard de la medie. Altfel spus, aceasta spune că 95% dintre măsurători se află în intervalul cuprins între:
\(\mu_{Y}- 2\sigma\) și \(\mu_{Y}+ 2\sigma\).
Aplicând regula 95% la exemplul nostru cu \(\mu_{Y} = 150\) și \(\sigma= 20\):
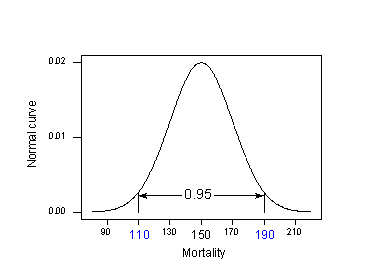
95% din ratele de mortalitate prin cancer de piele ale localităților aflate la 40 de grade latitudine nordică se află în intervalul cuprins între:
150 – 2(20) = 110 și 150 + 2(20) = 190.
Acest lucru înseamnă că, dacă cineva ar dori să cunoască rata mortalității prin cancer de piele pentru o locație situată la 40 de grade latitudine nordică, cea mai bună presupunere a noastră ar fi undeva între 110 și 190 decese la 10 milioane. Problema este că calculul nostru a folosit \(\mu_{Y}\) și \(\sigma\), valori ale populației pe care, în mod normal, nu le-am cunoaște. Realitatea se instalează:
- Media \(\mu_{Y}\) nu este de obicei cunoscută. Lucrul logic de făcut este să o estimăm cu ajutorul răspunsului prezis \(\hat{y}\). Costul utilizării \(\hat{y}\) pentru a estima \(\mu_{Y}\) este varianța lui \(\hat{y}\). Adică, eșantioane diferite ar produce predicții diferite \(\hat{y}\) și, prin urmare, trebuie să luăm în considerare această variație a \(\hat{y}\.
- Variația \( \sigma^{2}\) nu este de obicei cunoscută. Lucrul logic de făcut este să o estimăm cu MSE.
Pentru că trebuie să estimăm aceste cantități necunoscute, variația în predicția unui nou răspuns depinde de două componente:
- variația datorată estimării mediei \(\mu_{Y}\) cu \(\hat{y}_h\) , pe care o notăm „\(\sigma^2(\hat{Y}_h)\).” (Rețineți că estimarea acestei cantități este doar pătratul erorii standard de potrivire care apare în formula intervalului de încredere.)
- variația răspunsurilor y, pe care o notăm cu „\(\sigma^2\).” (Rețineți că această cantitate este estimată, ca de obicei, cu eroarea medie pătratică MSE.)
Adunând cele două componente de varianță, obținem:
\(\sigma^2+\sigma^2(\hat{Y}_h)\)
care este estimată prin:
(MSE+MSE \left( \dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \right) =MSE\left( 1+\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \right) \)
Recunoașteți această cantitate? Este doar varianța predicției care apare în formula pentru intervalul de predicție \(y_{new}\)!
Să comparăm din nou cele două intervale:
Intervalul de încredere pentru \(\mu_{Y}\colon \hat{y}_h \pm t_{(1-\alpha/2, n-2)} \times \sqrt{MSE \times \left( \frac{1}{n} + \frac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\dreapta)}\})}
Interval de predicție pentru \(y_{new}\colon \hat{y}_h \pm t_{(1-\alpha/2, n-2)} \times \sqrt{MSE \left( 1+\frac{1}{n} + \frac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\dreapta)}\})
Care sunt implicațiile practice ale diferenței dintre cele două formule?
- Pentru că intervalul de predicție are termenul suplimentar MSE, un interval de încredere \( \left( 1-\alpha \right) 100\% \) pentru \(\mu_{Y}\) la \(x_{h}\) va fi întotdeauna mai îngust decât intervalul de predicție \( \left( 1-\alpha \right) 100\% \) corespunzător \(y_{new}\) la \(x_{h}\).
- Calculând intervalul la media eșantionului pentru valorile predictorului \(\left(x_{h} = \bar{x}\right)\) și mărind dimensiunea eșantionului n, eroarea standard a intervalului de încredere se poate apropia de 0. Deoarece intervalul de predicție are termenul suplimentar MSE, eroarea standard a intervalului de predicție nu se poate apropia de 0.
Prima implicație este văzută cel mai ușor prin studierea următorului grafic pentru exemplul nostru de mortalitate prin cancer de piele:
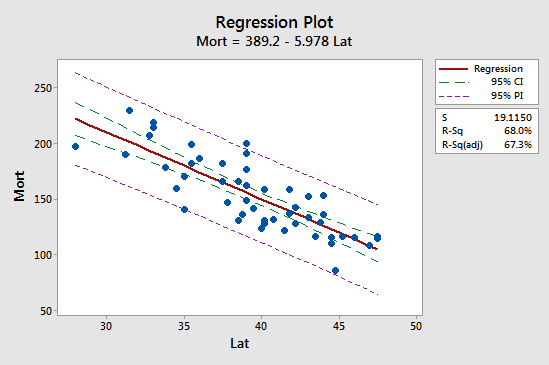
Observați că intervalul de predicție (IP 95%, în violet) este întotdeauna mai larg decât intervalul de încredere (IC 95%, în verde). Mai mult, ambele intervale sunt cele mai înguste la media valorilor predictorilor (aproximativ 39,5).
.