În această secțiune, vom învăța cum să găsim rădăcina (rădăcinile) unei ecuații pătratice. Rădăcinile se mai numesc și intersecții x sau zerouri. O funcție pătratică este reprezentată grafic de o parabolă cu vertexul situat la origine, sub axa x sau deasupra axei x. Prin urmare, o funcție pătratică poate avea una, două sau zero rădăcini.
Când ni se cere să rezolvăm o ecuație pătratică, ni se cere de fapt să găsim rădăcinile. Am văzut deja că completarea pătratului este o metodă utilă pentru a rezolva ecuațiile pătratice. Această metodă poate fi utilizată pentru a obține formula pătratică, care este utilizată pentru a rezolva ecuații pătratice. De fapt, rădăcinile funcției,
f (x) = ax2 + bx + c
sunt date de formula pătratică. Rădăcinile unei funcții sunt intersecțiile x. Prin definiție, coordonata y a punctelor situate pe axa x este zero. Prin urmare, pentru a găsi rădăcinile unei funcții pătratice, se stabilește f (x) = 0 și se rezolvă ecuația,
ax2 + bx + c = 0.
We can do this by completing the square as,
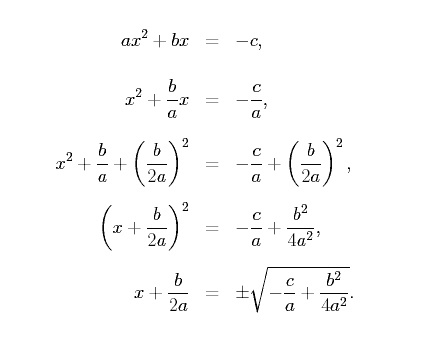
Solving for x and simplifying we have,
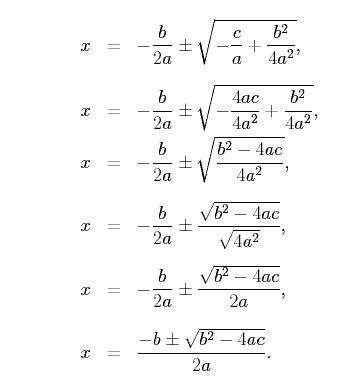
Thus, the roots of a quadratic function are given by,
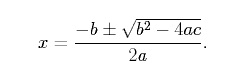
This formula is called the quadratic formula, and its derivation is included so that you can see where it comes from. We call the term b2 −4ac the discriminant. The discriminant is important because it tells you how many roots a quadratic function has. Specifically, if
1. b2 −4ac < 0 There are no real roots.
2. b2 −4ac = 0 There is one real root.
3. b2 −4ac > 0 There are two real roots.
We will examine each case individually.
Cazul 1: Nu există rădăcini reale
Dacă discriminantul unei funcții pătratice este mai mic decât zero, funcția respectivă nu are rădăcini reale, iar parabola pe care o reprezintă nu intersectează axa x. Deoarece formula pătratică necesită luarea rădăcinii pătrate a discriminantului, un discriminant negativ creează o problemă, deoarece rădăcina pătrată a unui număr negativ nu este definită pe linia reală. Un exemplu de funcție pătratică fără rădăcini reale este dat de:
f(x) = x2 – 3x + 4.
Observați că discriminantul lui f(x) este negativ,
b2 -4ac = (-3)2- 4 – 1 – 4 = 9 – 16 = -7.
Această funcție este reprezentată grafic de o parabolă care se deschide în sus și al cărei vârf se află deasupra axei x. Astfel, graficul nu poate intersecta niciodată axa x și nu are rădăcini, așa cum se arată mai jos,
Cazul 2: O singură rădăcină reală
Dacă discriminantul unei funcții pătratice este egal cu zero, funcția respectivă are exact o singură rădăcină reală și intersectează axa x într-un singur punct. Pentru a vedea acest lucru, setăm b2 -4ac = 0 în formula pătratică pentru a obține,
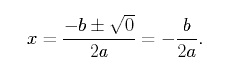
Observați că 
este coordonata x a vertexului unei parabole. Astfel, o parabolă are exact o rădăcină reală atunci când vertexul parabolei se află chiar pe axa x. Cel mai simplu exemplu de funcție pătratică care are o singură rădăcină reală este,
y = x2,
unde rădăcina reală este x = 0.
Un alt exemplu de funcție pătratică cu o singură rădăcină reală este dat de,
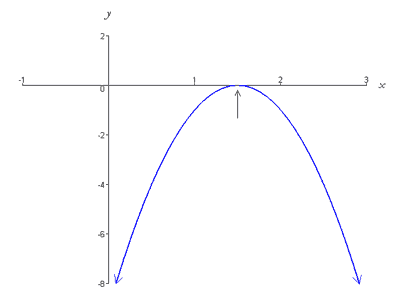
f(x) = -4×2 + 12x – 9.
Observați că discriminantul lui f(x) este zero,
b2 -4ac = (12)2- 4 – -4 – -9 = 144 – 144 = 0.
Această funcție este reprezentată grafic printr-o parabolă care se deschide în jos și are vertexul (3/2, 0), situat pe axa x. Thus, the graph intersects the x-axis at exactly one point (i.e. has one root) as shown below,
Case 3: Two Real Roots
If the discriminant of a quadratic function is greater than zero, that function has two real roots (x-intercepts). Taking the square root of a positive real number is well defined, and the two roots are given by,
An example of a quadratic function with two real roots is given by,
f(x) = 2×2− 11x + 5.
Notice that the discriminant of f(x) is greater than zero,