O funcție de producție Cobb-Douglas modelează relația dintre producția de producție și intrările de producție (factori). Este utilizată pentru a calcula raporturile dintre intrări și ieșiri pentru o producție eficientă și pentru a estima schimbările tehnologice în metodele de producție. Forma generală a unei funcții de producție Cobb-Douglas pentru un set de \(n\) intrări este\ unde \(Y\) reprezintă producția, \(x_{i}\) reprezintă intrarea \(i\), iar \(\gamma\) și \(\alpha_{i}\) sunt parametrii care determină eficiența globală a producției și capacitatea de reacție a producției la modificări ale cantităților de intrare. Aplicarea acestei forme funcționale în măsurarea producției se datorează matematicianului Charles Cobb și economistului Paul Douglas, care au utilizat-o pentru a analiza importanța relativă a celor doi factori de producție, munca și capitalul, în producția manufacturieră din SUA în perioada 1899-1922. În modelul lor original, Cobb și Douglas limitează parametrii de elasticitate a producției \(\alpha_{1}\) și \(\alpha_{2}\) la intervalul \(\alpha_{i}\in\left(0,1\right)\) și la suma de unu, ceea ce implică randamente constante la scară. Funcția este astfel\ unde \(x_{1}\) și \(x_{2}\) reprezintă munca și, respectiv, capitalul. Luând logaritmul natural al ambelor părți ale ecuației rezultă\ astfel încât, pentru datele privind producția, forța de muncă și capitalul, parametrii \(\gamma\) și \(\alpha_{1}\) pot fi estimați cu ajutorul celor mai mici pătrate ordinare. Pe baza datelor lor, Cobb și Douglas au găsit o valoare de 0,75 pentru \(\alpha_{1}\), ceea ce înseamnă că munca a reprezentat trei sferturi din valoarea producției manufacturiere din SUA (restul fiind reprezentat de capital) în perioada studiată. Estimarea lor pentru parametrul de eficiență \(\gamma\) este de 1,01, care, întrucât este mai mare decât 1, reflectă efectele pozitive ale forțelor neobservabile asupra producției prin combinarea muncii și a capitalului.
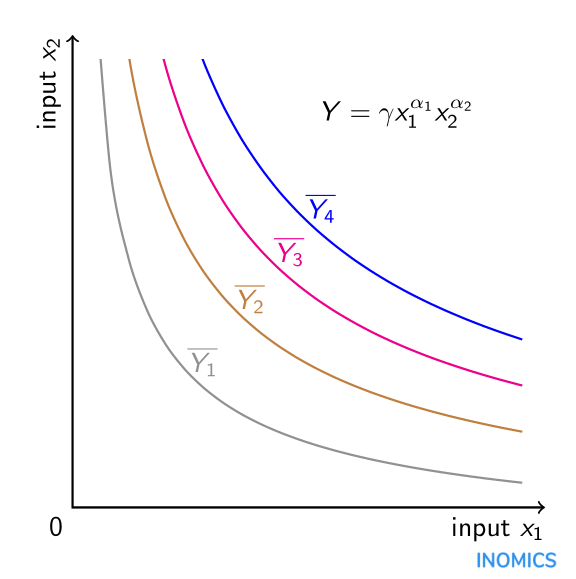
Natura multiplicativă a unei funcții de producție Cobb-Douglas, presupunând valori pozitive pentru \(\alpha_{i}\), înseamnă că factorii de producție sunt complementari în producție. În modelul standard al muncii și capitalului, creșterea cantității de capital mărește producția nu numai în mod direct, ci și indirect, prin impactul său asupra productivității muncii. Din punct de vedere matematic, derivata parțială încrucișată a producției \(Y\) în raport cu forța de muncă \(x_{1}\) și capitalul \(x_{2}\) este pozitivă. În plus, datorită ipotezei că \(\(\alpha_{i}\în\stânga(0,1\dreapta)\), derivatele parțiale de ordinul doi ale producției în raport cu forța de muncă și în raport cu capitalul sunt ambele negative, ceea ce implică randamente marginale descrescătoare pentru fiecare factor de producție în parte. Simpla adăugare fie a mai multă muncă, fie a mai mult capital (dar nu a ambelor) în procesul de producție mărește producția, dar cu o rată descrescătoare. În plus, elasticitatea de substituție între factorii de producție este constantă și egală cu unu datorită formei funcționale. O funcție de producție Cobb-Douglas cu două intrări poate fi reprezentată grafic sub forma unor izocuante: combinații ale ambelor intrări pentru care producția este constantă. În graficul de față există patru astfel de izocuante pentru nivelurile de producție (constante) \(\supralinie{Y_{1}}\), \(\supralinie{Y_{2}}\), \(\supralinie{Y_{3}}\) și \(\supralinie{Y_{4}}\). Cu cât izocuanta este mai departe de origine, cu atât mai mare este nivelul producției \(\overline{Y_{4}}>\overline{Y_{3}}>\overline{Y_{2}}>\overline{Y_{1}}\). Combinația precisă dintre inputurile \(x_{1}\) și \(x_{2}\) care este optimă pentru producție este determinată de bugetul de care dispune producătorul, precum și de raportul dintre costul inputului \(x_{2}\) și inputul \(x_{1}\), care poate fi inclus în grafic sub forma unei linii de izocost (a se vedea articolul privind elasticitatea de substituție).
Cobb și Douglas au recunoscut ei înșiși că funcția lor de producție nu se bazează pe fundamente teoretice solide și nici nu trebuie înțeleasă ca o lege a producției; ea reprezintă doar o aproximare statistică a relațiilor observate între intrările și ieșirile de producție. Cu toate acestea, proprietățile sale matematice simple sunt atractive pentru economiști și au făcut ca aceasta să devină un standard în teoria microeconomică în ultimul secol.
Lectură suplimentară:
Pentru contextul și o prezentare generală a principalelor proprietăți ale funcțiilor de producție Cobb-Douglas, a se vedea în special secțiunile 6, 7 și 8 din articolul original al lui Cobb și Douglas, „A Theory of Production” (The American Economic Review, 1928).
Bine de știut:
Forma funcțională Cobb-Douglas nu este utilizată doar în teoria producției, ci a devenit standard și în teoria microeconomică a consumatorului, unde este aplicată ca funcție de utilitate, unde \(Y\) devine \(U\) pentru utilitate. \(x_{i}\) reprezintă apoi elementele de consum și, atunci când funcția de utilitate este maximizată sub rezerva unei constrângeri bugetare, valorile pentru \(\alpha_{i}\) indică modul în care individul va distribui în mod optim bugetul între articole.
.