Pătratele magice sunt grile pătrate cu un aranjament special de numere în ele. Aceste numere sunt speciale pentru că fiecare rând, coloană și diagonală însumează același număr. Așadar, pentru exemplul de mai jos, 15 este numărul magic. Ați putea să vă dați seama de acest lucru doar știind că pătratul folosește numerele de la 1 la 9?

De asemenea, cele două numere care sunt opuse unul față de celălalt peste numărul central se vor aduna la același număr. Astfel, în pătratul de mai sus, 8 + 2 = 10 , 6 + 4 = 10, 1 + 9 = 10 și 3 + 7 = 10. De ce se întâmplă acest lucru?
„Ordinea” unui pătrat magic spune câte rânduri sau coloane are. Astfel, un pătrat cu 3 rânduri și coloane este de ordinul 3, iar un pătrat cu 4 rânduri și coloane este de ordinul 4 și așa mai departe. Dacă doriți să aflați mai multe despre cum să vă confecționați propriile pătrate magice și despre matematica din spatele acestora, puteți accesa alte pagini de pe site, cum ar fi Pătrate magice și Pătrate magice II.
Dar de ce se numesc magice?
Dar numerele din pătratul magic sunt speciale, dar de ce se numesc magice? Se pare că din cele mai vechi timpuri au fost conectate cu lumea supranaturală și magică. Cea mai veche înregistrare a pătratelor magice provine din China, în jurul anului 2200 î.Hr. și se numește „Lo-Shu”. Există o legendă care spune că Împăratul Yu a văzut acest pătrat magic pe spatele unei broaște țestoase divine în Râul Galben.
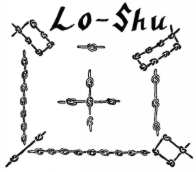
Nodurile negre arată numerele pare, iar cele albe arată numerele impare. Priviți cu atenție și veți vedea că acest pătrat magic antic este același cu exemplul nostru de mai sus. Pătratele magice au fost menționate pentru prima dată în lumea occidentală în lucrarea lui Theon din Smirna. Ele au fost, de asemenea, folosite de astrologii arabi în secolul al IX-lea pentru a ajuta la elaborarea horoscopurilor. Lucrările matematicianului grec Moschopoulos din anul 1300 d.Hr. au contribuit la răspândirea cunoștințelor despre pătratele magice. Așa că iată-ne acum, mai bine de 700 de ani mai târziu, iar profesorii le folosesc în clasă pentru rezolvarea problemelor și exersarea adunării.
Puteți realiza pătrate magice similare, de ordinul 3, folosind numere diferite. Vedeți vreun model în numerele care funcționează?
.