Proiecții
Acum că am descris conceptul de reducere a dimensiunii și unele dintre aplicațiile SVD și ale analizei componentelor principale, ne concentrăm pe mai multe detalii legate de matematica din spatele acestora. Începem cu proiecțiile. O proiecție este un concept de algebră liniară care ne ajută să înțelegem multe dintre operațiile matematice pe care le efectuăm asupra datelor cu dimensiuni mari. Pentru mai multe detalii, puteți revizui proiectele într-o carte de algebră liniară. Aici oferim o scurtă trecere în revistă și apoi oferim câteva exemple legate de analiza datelor.
Ca o trecere în revistă, amintiți-vă că proiecțiile minimizează distanța dintre puncte și subspațiu.

În figura de mai sus, punctul din partea de sus arată spre un punct din spațiu. În această caricatură particulară, spațiul este bidimensional, dar ar trebui să gândim în mod abstract. Spațiul este reprezentat de planul cartezian, iar linia pe care se află micuța persoană este un subspațiu de puncte. Proiecția în acest subspațiu este locul care este cel mai apropiat de punctul original. Geometria ne spune că putem găsi acest punct cel mai apropiat prin coborârea unei linii perpendiculare (linie punctată) de la punctul respectiv la spațiu. Persoana mică se află pe proiecție. Cantitatea pe care această persoană a trebuit să o parcurgă de la origine până la noul punct proiectat se numește coordonată.
Pentru explicarea proiecțiilor, vom folosi notația standard de algebră matriceală pentru puncte: este un punct în spațiul -dimensional și este subspațiul mai mic.
Exemplu simplu cu N=2
Dacă lăsăm . Îl putem reprezenta grafic astfel:
mypar (1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)text(2,3," Y",pos=4,cex=3)
Potem defini imediat un sistem de coordonate prin proiectarea acestui vector în spațiul definit de: (axa x) și (axa y). Proiecțiile lui în subspațiul definit de aceste puncte sunt 2 și, respectiv, 3:
Spunem că și sunt coordonatele și că sunt bazele.
Acum să definim un nou subspațiu. Linia roșie din graficul de mai jos este subspațiul definit de punctele care satisfac cu . Proiecția lui onto este cel mai apropiat punct de pe . Așadar, trebuie să găsim care minimizează distanța dintre și . În algebra liniară, învățăm că diferența dintre aceste puncte este ortogonală spațiului astfel încât:
acest lucru implică faptul că:
și:
Aici punctul reprezintă produsul de puncte: .
Codul R următor confirmă că această ecuație funcționează:
mypar(1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)abline(0,0.5,col="red",lwd=3) #if x=2c and y=c then slope is 0.5 (y=0.5x)text(2,3," Y",pos=4,cex=3)y=c(2,3)x=c(2,1)cc = crossprod(x,y)/crossprod(x)segments(x*cc,x*cc,y,y,lty=2)text(x*cc,x*cc,expression(hat(Y)),pos=4,cex=3)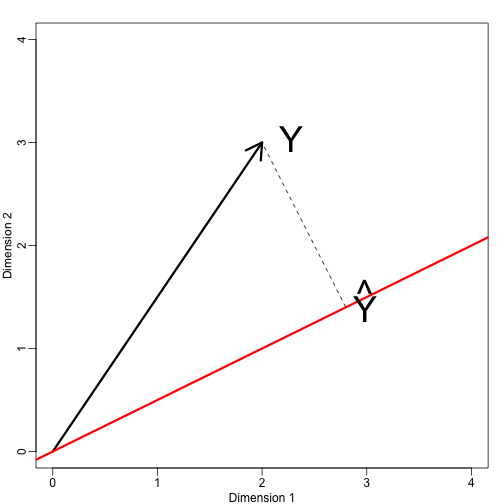
Rețineți că dacă a fost astfel încât , atunci este pur și simplu și spațiul nu se schimbă. Această simplificare este unul dintre motivele pentru care ne plac matricile ortogonale.
Exemplu: Media eșantionului este o proiecție
După ce și este spațiul cuprins de:
În acest spațiu, toate componentele vectorilor au același număr, astfel încât ne putem gândi la acest spațiu ca reprezentând constantele: în proiecție fiecare dimensiune va avea aceeași valoare. Deci, ce minimizează distanța dintre și ?
Când vorbim despre probleme de acest gen, folosim uneori figuri bidimensionale precum cea de mai sus. Pur și simplu facem abstracție și ne gândim la un punct în și ca la un subspațiu definit de un număr mai mic de valori, în acest caz doar una singură: .
Răspunzând la întrebarea noastră, știm că proiecția este:
care în acest caz este media:
Aici, de asemenea, ar fi fost la fel de ușor să folosim calculul:
Exemplu: Regresia este, de asemenea, o proiecție
Să dăm un exemplu ceva mai complicat. Regresia liniară simplă poate fi explicată și cu ajutorul proiecțiilor. Datele noastre (nu vom mai folosi această notație) sunt din nou un vector, iar modelul nostru prezice cu o dreaptă . We want to find the and that minimize the distance between and the space defined by:
with:
Our matrix is and any point in can be written as .
The equation for the multidimensional version of orthogonal projection is:
which we have seen before and gives us:
And the projection to is therefore: