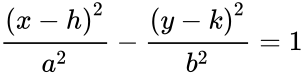by: adminPosted on:

Semi-Majorachse

Datei:Semimajorachse.png

Die semimajorale Achse einer Ellipse

In der Geometrie wird der Begriff semimajorale Achse (auch semimajorale Achse) zur Beschreibung der Abmessungen von Ellipsen und Hyperbeln verwendet.

Ellipse

Die Hauptachse einer Ellipse ist ihr längster Durchmesser, eine Linie, die durch den Mittelpunkt und die beiden Brennpunkte verläuft und deren Enden an den breitesten Punkten der Form liegen. Die Halbachse ist die Hälfte der Hauptachse und verläuft somit vom Zentrum durch einen Brennpunkt zum Rand der Ellipse.

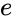
Sie ist mit der Halbnebenachse {\displaystyle b\,\!} durch die Exzentrizität {\displaystyle e\,\!} und den Halblatus rectum {\displaystyle \ell \,\!}, wie folgt:

{\displaystyle b=a{\sqrt {1-e^{2}}\,\!}{\displaystyle \ell =a(1-e^{2})\,\!}{\displaystyle a\ell =b^{2}\,\!}.

Eine Parabel erhält man als Grenzwert einer Folge von Ellipsen, bei denen ein Brennpunkt fixiert bleibt, während sich der andere beliebig weit in eine Richtung entfernen kann, wobei {\displaystyle \ell \,\!} fixiert bleibt. So tendieren {\displaystyle a\,\!} und {\displaystyle b\,\!} ins Unendliche, {\displaystyle a\,\!} schneller als {\displaystyle b\,\!}.

Die Halbachse ist der Mittelwert der kleinsten und größten Abstände von einem Brennpunkt zu den Punkten der Ellipse. Betrachten wir nun die Gleichung in Polarkoordinaten, wobei ein Brennpunkt im Ursprung und der andere auf der positiven x-Achse liegt,

{\displaystyle r(1-e\cos \theta )=l\,\!}

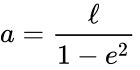
The mean value of {\displaystyle r={\ell \over {1+e}}\,\!} and {\displaystyle r={\ell \over {1-e}}\,\!}, is {\displaystyle a={\ell \over {1-e^{2}}}\,\!}.

Hyperbola

The semi-major axis of a hyperbola is one half of the distance between the two branches; if this is a in the x-direction the equation is:

{\displaystyle {\frac {\left(x-h\right)^{2}}{a^{2}}}-{\frac {\left(y-k\right)^{2}}{b^{2}}}=1}

In terms of the semi-latus rectum and the eccentricity we have

{\displaystyle a={\ell \over e^{2}-1}}

Astronomy

Orbital period

In astrodynamics the orbital period 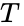{\displaystyle T\,} of a small body orbiting a central body in a circular or elliptical orbit is:

{\displaystyle T=2\pi {\sqrt {a^{3}/\mu }}}

where:

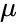
{\displaystyle a\,}ist die Länge der Halbachse der Bahn{\displaystyle \mu }ist der Standardgravitationsparameter

Beachte, dass für alle Ellipsen mit einer gegebenen Halbachse die Bahnperiode gleich ist, unabhängig von der Exzentrizität.

In der Astronomie ist die Halbachse neben der Umlaufzeit eines der wichtigsten Elemente einer Umlaufbahn. Bei Objekten des Sonnensystems wird die Halbachse durch das (ursprünglich empirisch abgeleitete) dritte Keplersche Gesetz mit der Periode der Umlaufbahn in Beziehung gesetzt,

{\displaystyle T^{2}=a^{3}\,}

wobei T die Periode in Jahren und a die Halbachse in astronomischen Einheiten ist. Diese Form erweist sich als eine Vereinfachung der allgemeinen Form für das Zweikörperproblem, wie sie von Newton festgelegt wurde:

{\displaystyle T^{2}={\frac {4\pi ^{2}}{G(M+m)}}a^{3}\,}

wobei G die Gravitationskonstante ist und M die Masse des Zentralkörpers und m die Masse des umlaufenden Körpers ist. Normalerweise ist die Masse des Zentralkörpers so viel größer als die des umkreisenden Körpers, dass m ignoriert werden kann. Unter dieser Annahme und bei Verwendung der in der Astronomie üblichen Einheiten ergibt sich die einfachere Form, die Kepler entdeckt hat.

Besonders bemerkenswert ist, dass sowohl die Bahn des umlaufenden Körpers um das Baryzentrum als auch seine Bahn relativ zu seinem Primärkörper Ellipsen sind. Die in der Astronomie verwendete Halbachse ist immer der Abstand von Primär zu Sekundär; daher werden die Bahnparameter der Planeten in heliozentrischen Begriffen angegeben. Der Unterschied zwischen der primozentrischen und der „absoluten“ Umlaufbahn lässt sich am besten am Beispiel des Systems Erde-Mond veranschaulichen. Das Massenverhältnis beträgt in diesem Fall 81,30059. Der charakteristische Abstand Erde-Mond, die Halbachse der geozentrischen Mondbahn, beträgt 384.400 km. Die baryzentrische Mondbahn hingegen hat eine Halbachse von 379.700 km, wobei die Gegenbahn der Erde die Differenz von 4.700 km ausmacht. Die durchschnittliche baryzentrische Bahngeschwindigkeit des Mondes beträgt 1,010 km/s, die der Erde 0,012 km/s. Die Summe dieser Geschwindigkeiten ergibt die geozentrische Durchschnittsgeschwindigkeit des Mondes, 1,022 km/s; den gleichen Wert erhält man, wenn man nur den Wert der geozentrischen Halbachse betrachtet.

Durchschnittliche Entfernung

Es wird oft gesagt, dass die Halbachse die „durchschnittliche“ Entfernung zwischen dem Primärkreis (dem Brennpunkt der Ellipse) und dem umlaufenden Körper ist. Das ist nicht ganz richtig, da es davon abhängt, worüber der Mittelwert gebildet wird.

  • Die Mittelung des Abstands über die exzentrische Anomalie (siehe oben) ergibt in der Tat die Semi-Hauptachse.
  • Die Mittelwertbildung über die wahre Anomalie (den wahren Bahnwinkel, gemessen im Brennpunkt) ergibt seltsamerweise die halbminore Achse {\displaystyle b=a{\sqrt {1-e^{2}}},\!}.
  • Die Mittelung über die mittlere Anomalie (der Bruchteil der Umlaufzeit, der seit dem Perizentrum verstrichen ist, ausgedrückt als Winkel) ergibt schließlich den Zeitdurchschnitt (was für den Laien gewöhnlich „Durchschnitt“ bedeutet): {\displaystyle a(1+{\frac {e^{2}}{2}})\,\!}.

Der zeitliche Mittelwert der Inverse des Radius, {\displaystyle r^{-1}\,\!}, ist {\displaystyle a^{-1}\,\!}.

Energie; Berechnung der Halbachse aus Zustandsvektoren

In der Astrodynamik kann die Halbachse {\displaystyle a\,} aus orbitalen Zustandsvektoren berechnet werden:

{\displaystyle a={-\mu \over {2\epsilon }}\,} for an elliptical orbit and {\displaystyle a={\mu \over {2\epsilon }}\,} for a hyperbolic trajectory

and

{\displaystyle \epsilon ={v^{2} \over {2}}-{\mu \over \left|\mathbf {r} \right|}} (specific orbital energy)

and

{\displaystyle \mu =GM\,} (standard gravitational parameter),

where:

  • {\displaystyle v\,} is orbital velocity from velocity vector of an orbiting object,
  • {\displaystyle \mathbf {r} \,} is cartesian position vector of an orbiting object in coordinates of a reference frame with respect to which the elements of the orbit are to be calculated (e.g. geozentrisch äquatorial für eine Umlaufbahn um die Erde oder heliozentrisch ekliptisch für eine Umlaufbahn um die Sonne),
  • {\displaystyle G\,} ist die Gravitationskonstante,
  • {\displaystyle M\,} die Masse des Zentralkörpers.

Bei einem gegebenen Zentralkörper und einer gegebenen spezifischen Gesamtenergie ist die Halbachse unabhängig von der Exzentrizität immer gleich groß. Umgekehrt ist für einen gegebenen Zentralkörper und eine gegebene Halbachse die gesamte spezifische Energie immer gleich.

Beispiel

Die Internationale Raumstation hat eine Umlaufzeit von 91,74 Minuten, daher beträgt die Halbachse 6738 km. Jede Minute mehr entspricht ca. 50 km mehr: Für die zusätzlichen 300 km Bahnlänge werden 40 Sekunden benötigt, die geringere Geschwindigkeit schlägt mit 20 Sekunden zu Buche.

Schreibe einen Kommentar

Deine E-Mail-Adresse wird nicht veröffentlicht. Erforderliche Felder sind mit * markiert.