V naší diskusi o intervalu spolehlivosti pro \(\mu_{Y}\) jsme použili vzorec ke zjištění, jaké faktory ovlivňují šířku intervalu spolehlivosti. Není třeba to dělat znovu. Protože vzorce jsou si velmi podobné, ukazuje se, že faktory ovlivňující šířku předpovědního intervalu jsou totožné s faktory ovlivňujícími šířku intervalu spolehlivosti.
Prozkoumejme místo toho vzorec pro předpovědní interval pro \(y_{new}\):
\(\hat{y}_h \pm t_{(1-\alfa/2, n-2)} \krát \sqrt{MSE \krát \left( 1+\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\)
pro srovnání se vzorcem pro interval spolehlivosti pro \(\mu_{Y}\):
\(\hat{y}_h \pm t_{(1-\alfa/2, n-2)} \krát \sqrt{MSE \left(\dfrac{1}{n}) + \dfrac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\)
Všimněte si, že jediný rozdíl ve vzorcích spočívá v tom, že standardní chyba předpovědi pro \(y_{new}\) má navíc člen MSE, který standardní chyba shody pro \(\mu_{Y}\) nemá.
Pokusme se pochopit interval předpovědi, abychom zjistili, co způsobuje dodatečný člen MSE. Začněme přitom nejprve s jednodušším problémem. Zamysleme se nad tím, jak bychom mohli předpovědět novou odezvu \(y_{new}\) při určité hodnotě \(x_{h}\), kdybychom znali střední hodnotu odezvy \(\mu_{Y}\) při hodnotě \(x_{h}\). To znamená, předpokládejme, že je známo, že průměrná úmrtnost na rakovinu kůže při \(x_{h} = 40^{o}\) N je 150 úmrtí na milion (s rozptylem 400)? Jaká je předpokládaná úmrtnost na rakovinu kůže ve městě Columbus ve státě Ohio?
Protože známe \(\mu_{Y} = 150 \) a \( \sigma^{2} = 400 \), můžeme využít „empirické pravidlo“, které mimo jiné říká, že 95 % měření normálně rozdělených dat je v rozmezí 2 směrodatných odchylek od průměru. To znamená, že 95 % měření se nachází v intervalu mezi:
\(\mu_{Y}- 2\sigma\) a \(\mu_{Y}+ 2\sigma\).
Při použití 95% pravidla na náš příklad s \(\mu_{Y} = 150\) a \(\sigma= 20\):
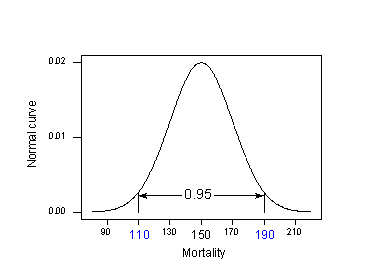
95 % úmrtnosti na rakovinu kůže v lokalitách na 40 stupních severní šířky se nachází v intervalu sevřeném:
150 – 2(20) = 110 a 150 + 2(20) = 190.
Normální křivka vs. graf úmrtnosti.
To znamená, že pokud by někdo chtěl znát míru úmrtnosti na rakovinu kůže pro lokalitu na 40 stupních severní šířky, náš nejlepší odhad by byl někde mezi 110 a 190 úmrtími na 10 milionů. Problém je v tom, že náš výpočet použil \(\mu_{Y}\) a \(\sigma\), což jsou populační hodnoty, které obvykle neznáme. Realita je následující:
- Střední hodnotu \(\mu_{Y}\) obvykle neznáme. Logické je odhadnout ji pomocí předpokládané odezvy \(\hat{y}\). Cena použití \(\hat{y}\) k odhadu \(\mu_{Y}\) je rozptyl \(\hat{y}\). To znamená, že různé vzorky by daly různé předpovědi \(\hat{y}\), a proto musíme vzít v úvahu tento rozptyl \(\hat{y}\).
- Rozptyl \( \sigma^{2}\) obvykle není znám. Logické je odhadnout ji pomocí MSE.
Protože musíme tyto neznámé veličiny odhadnout, závisí odchylka v předpovědi nové odpovědi na dvou složkách:
- odchylka způsobená odhadem střední hodnoty \(\mu_{Y}}) s \(\hat{y}_h\) , kterou označujeme „\(\sigma^2(\hat{Y}_h)\).“ (Všimněte si, že odhad této veličiny je pouze čtverec standardní chyby shody, který se objevuje ve vzorci intervalu spolehlivosti.)
- změna odpovědí y, kterou označujeme jako „\(\sigma^2\).“ (Všimněte si, že tato veličina se jako obvykle odhaduje pomocí střední kvadratické chyby MSE.)
Přičteme-li obě složky rozptylu, dostaneme:
\(\sigma^2+\sigma^2(\hat{Y}_h)\)
která se odhaduje pomocí:
\(MSE+MSE \left( \dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \pravá) =MSE\levá( 1+\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \right) \)
Poznáváte tuto veličinu? Je to právě rozptyl předpovědi, který se objevuje ve vzorci pro interval předpovědi \(y_{new}\)!
Pokusme se znovu porovnat oba intervaly:
Interval spolehlivosti pro \(\mu_{Y}\colon \hat{y}_h \pm t_{(1-\alfa/2, n-2)} \krát \sqrt{MSE \krát \left( \frac{1}{n} + \frac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\)
Předpovědní interval pro \(y_{new}\colon \hat{y}_h \pm t_{(1-\alfa/2, n-2)} \krát \sqrt{MSE \left( 1+\frac{1}{n} + \frac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\)
Jaké jsou praktické důsledky rozdílu v obou vzorcích?
- Protože interval předpovědi obsahuje další člen MSE, bude interval spolehlivosti \( \left( 1-\alfa \right) 100\% \) pro \(\mu_{Y}\) při \(x_{h}\) vždy užší než odpovídající interval předpovědi \( \left( 1-\alfa \right) 100\% \) pro \(y_{new}\) při \(x_{h}\).
- Výpočtem intervalu při střední hodnotě prediktoru ve vzorku \(\left(x_{h} = \bar{x}\right)\) a zvětšením velikosti vzorku n se může směrodatná chyba intervalu spolehlivosti přiblížit k 0. Protože interval predikce má navíc člen MSE, nemůže se směrodatná chyba intervalu predikce přiblížit k 0.
První důsledek je nejsnáze patrný při studiu následujícího grafu pro náš příklad úmrtnosti na rakovinu kůže:
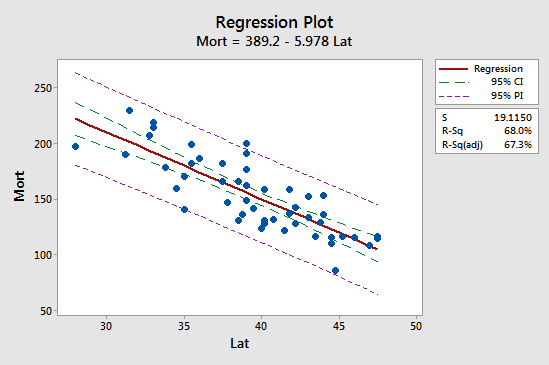
Všimněte si, že interval předpovědi (95% PI, fialově) je vždy širší než interval spolehlivosti (95% CI, zeleně). Oba intervaly jsou navíc nejužší u střední hodnoty prediktoru (přibližně 39,5).