V této části se naučíme najít kořeny kvadratické rovnice. Kořeny se také nazývají x-intercepty nebo nuly. Kvadratická funkce je graficky znázorněna parabolou s vrcholem umístěným v počátku, pod osou x nebo nad osou x. Kvadratickou funkci lze graficky znázornit jako parabolu s vrcholem umístěným v počátku. Kvadratická funkce tedy může mít jeden, dva nebo nulové kořeny.
Když máme vyřešit kvadratickou rovnici, ve skutečnosti se po nás chce, abychom našli kořeny. Již jsme viděli, že doplnění čtverce je užitečná metoda řešení kvadratických rovnic. Tuto metodu lze použít k odvození kvadratického vzorce, který se používá k řešení kvadratických rovnic. Kořeny funkce
f (x) = ax2 + bx + c
jsou vlastně dány kvadratickým vzorcem. Kořeny funkce jsou průsečíky x. Podle definice je y-ová souřadnice bodů ležících na ose x nulová. Chceme-li tedy najít kořeny kvadratické funkce, zadáme f (x) = 0 a vyřešíme rovnici,
ax2 + bx + c = 0.
We can do this by completing the square as,
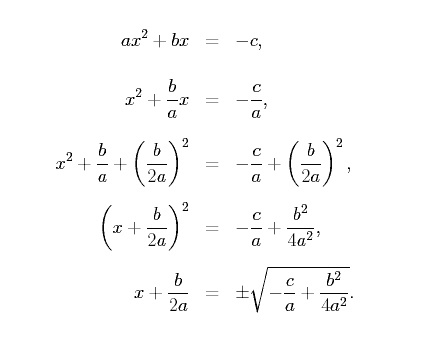
Solving for x and simplifying we have,
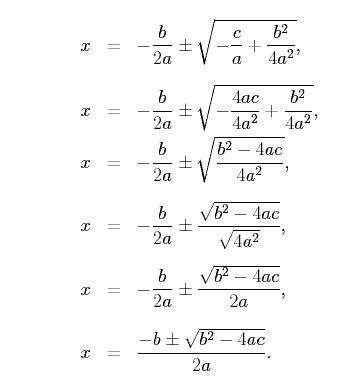
Thus, the roots of a quadratic function are given by,
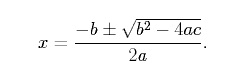
This formula is called the quadratic formula, and its derivation is included so that you can see where it comes from. We call the term b2 −4ac the discriminant. The discriminant is important because it tells you how many roots a quadratic function has. Specifically, if
1. b2 −4ac < 0 There are no real roots.
2. b2 −4ac = 0 There is one real root.
3. b2 −4ac > 0 There are two real roots.
We will examine each case individually.
Případ 1: Žádné reálné kořeny
Pokud je diskriminant kvadratické funkce menší než nula, nemá tato funkce žádné reálné kořeny a parabola, kterou představuje, neprotíná osu x.
Pokud je diskriminant kvadratické funkce menší než nula, nemá tato funkce žádné reálné kořeny. Protože kvadratický vzorec vyžaduje vzít druhou odmocninu diskriminantu, záporný diskriminant vytváří problém, protože druhá odmocnina záporného čísla není definována nad reálnou přímkou. Příklad kvadratické funkce, která nemá reálné kořeny, je dán vztahem:
f(x) = x2 – 3x + 4 .
Poznamenejme, že diskriminant funkce f(x) je záporný,
b2 -4ac = (-3)2- 4 – 1 – 4 = 9 – 16 = -7.
Tuto funkci graficky znázorňuje parabola, která se otevírá směrem vzhůru a jejíž vrchol leží nad osou x. Graf tedy nikdy nemůže protínat osu x a nemá žádné kořeny, jak ukazuje následující obrázek
Případ 2: Jeden reálný kořen
Je-li diskriminant kvadratické funkce roven nule, má tato funkce právě jeden reálný kořen a protíná osu x v jediném bodě. Abychom se o tom přesvědčili, nastavíme v kvadratickém vzorci b2 -4ac = 0 a dostaneme:
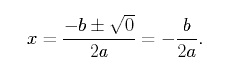
Všimněte si, že 
je x-ová souřadnice vrcholu paraboly. Parabola má tedy přesně jeden reálný kořen, když vrchol paraboly leží přímo na ose x. Nejjednodušším příkladem kvadratické funkce, která má pouze jeden reálný kořen, je,
y = x2,
kde reálný kořen je x = 0.
Další příklad kvadratické funkce s jedním reálným kořenem je dán vztahem,
f(x) = -4×2 + 12x – 9.
Všimněte si, že diskriminant funkce f(x) je nulový,
b2 -4ac = (12)2- 4 – -4 – -9 = 144 – 144 = 0.
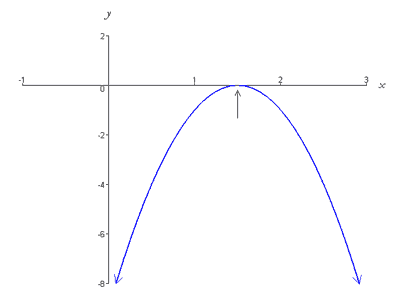
Tuto funkci graficky znázorňuje parabola, která se otevírá směrem dolů a má vrchol (3/2, 0), ležící na ose x.
Tato funkce je graficky znázorněna parabolou, která se otevírá směrem dolů. Thus, the graph intersects the x-axis at exactly one point (i.e. has one root) as shown below,
Case 3: Two Real Roots
If the discriminant of a quadratic function is greater than zero, that function has two real roots (x-intercepts). Taking the square root of a positive real number is well defined, and the two roots are given by,
An example of a quadratic function with two real roots is given by,
f(x) = 2×2− 11x + 5.
Notice that the discriminant of f(x) is greater than zero,