Cobb-Douglasova produkční funkce modeluje vztah mezi výstupem výroby a výrobními vstupy (faktory). Používá se k výpočtu vzájemných poměrů vstupů pro efektivní výrobu a k odhadu technologických změn ve výrobních metodách. Obecný tvar Cobb-Douglasovy výrobní funkce pro soubor vstupů \(n\) je\, kde \(Y\) znamená výstup, \(x_{i}\) vstup \(i\) a \(\gamma\) a \(\alfa_{i}\) jsou parametry určující celkovou efektivnost výroby a reakci výstupu na změny množství vstupů. Za použití této funkční formy při měření výroby vděčíme matematikovi Charlesi Cobbovi a ekonomovi Paulu Douglasovi, kteří ji použili k posouzení relativního významu dvou vstupních faktorů, práce a kapitálu, ve výrobě v USA v období 1899 až 1922. Ve svém původním modelu Cobb a Douglas omezili parametry pružnosti výstupu \(\alfa_{1}\) a \(\alfa_{2}\) na rozsah \(\alfa_{i}\in\left(0,1\right)\) a na součet jedna, což znamená konstantní výnosy z rozsahu. Funkce je tedy\, kde \(x_{1}\) a \(x_{2}\) znamenají práci a kapitál. Vezmeme-li přirozený logaritmus obou stran rovnice, dostaneme výnosy, takže pro údaje o produkci, práci a kapitálu lze parametry \(\gamma\) a \(\alfa_{1}\) odhadnout pomocí obyčejných nejmenších čtverců. Na základě svých údajů Cobb a Douglas zjistili, že hodnota \(\alpha_{1}\) je 0,75, což znamená, že na práci připadají tři čtvrtiny hodnoty výrobní produkce USA (na kapitál připadá zbývající čtvrtina) ve sledovaném období. Jejich odhad parametru efektivnosti \(\gamma\) je 1,01, což vzhledem k tomu, že je větší než 1, odráží pozitivní vliv nepozorovatelných sil na výrobu prostřednictvím kombinace práce a kapitálu.
Multiplikativní povaha Cobb-Douglasovy produkční funkce za předpokladu kladných hodnot \(\alpha_{i}\) znamená, že vstupy se ve výrobě doplňují. Ve standardním modelu práce a kapitálu zvyšuje zvyšování množství kapitálu produkci nejen přímo, ale také nepřímo prostřednictvím svého vlivu na produktivitu práce. Matematicky je křížová parciální derivace výstupu výroby \(Y\) vzhledem k práci \(x_{1}\) a kapitálu \(x_{2}\) kladná. Navíc vzhledem k předpokladu, že \(\alfa_{i}\in\left(0,1\right)\), jsou parciální derivace druhého řádu výstupu výroby vzhledem k práci a vzhledem ke kapitálu záporné, což znamená, že pouze pro každý vstup klesají mezní výnosy. Pouhé přidání buď více práce, nebo více kapitálu (ale ne obojího) do výrobního procesu zvyšuje výstup, avšak s klesající mírou. Kromě toho je elasticita substituce mezi vstupy konstantní a vzhledem k funkční formě se rovná jedné. Cobb-Douglasovu produkční funkci se dvěma vstupy lze graficky znázornit ve formě izokvant: kombinací obou vstupů, pro které je výstup konstantní. V grafu jsou čtyři takové izokvanty pro (konstantní) úrovně výstupu \(\overline{Y_{1}}), \(\overline{Y_{2}}), \(\overline{Y_{3}}) a \(\overline{Y_{4}}). Čím dále je izokvanta od počátku, tím větší je úroveň výstupu \(\overline{Y_{4}}>\overline{Y_{3}}>\overline{Y_{2}}>\overline{Y_{1}}). Která přesná kombinace vstupů \(x_{1}\) a \(x_{2}\) je pro výrobu optimální, je určeno rozpočtem, který má výrobce k dispozici, a také poměrem nákladů vstupu \(x_{2}\) ke vstupu \(x_{1}\), který lze do grafu zahrnout v podobě přímky izokladů (viz článek o elasticitě substituce).
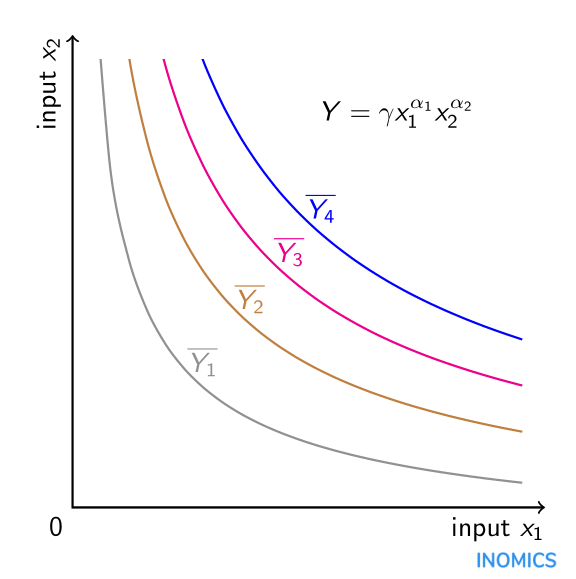
Cobb a Douglas sami přiznávají, že jejich produkční funkce nestojí na pevných teoretických základech a neměla by být chápána jako zákon výroby; představuje pouze statistickou aproximaci pozorovaných vztahů mezi výrobními vstupy a výstupem. Přesto jsou její jednoduché matematické vlastnosti pro ekonomy přitažlivé a vedly k tomu, že se v minulém století stala standardem v mikroekonomické teorii.
Další čtení:
Odůvodnění a přehled hlavních vlastností Cobbovy-Douglasovy produkční funkce viz zejména oddíly 6, 7 a 8 původního článku Cobba a Douglase „A Theory of Production“ (The American Economic Review, 1928).
Dobré vědět:
Cobb-Douglasova funkční forma se používá nejen v teorii výroby, ale stala se také standardem v mikroekonomické teorii spotřebitele, kde se používá jako funkce užitku, kde se \(Y\) stává \(U\) pro užitek. Hodnoty \(x_{i}\) pak představují položky spotřeby, a pokud je funkce užitku maximalizována s ohledem na rozpočtové omezení, hodnoty \(\alfa_{i}\) ukazují, jak jednotlivec optimálně rozdělí rozpočet mezi položky.