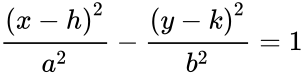by: adminPosted on:

Polomajoritní osa

File:Semimajoraxis.png

Poloměrná osa elipsy

V geometrii se termín poloměrná osa (také semimajorní osa) používá pro popis rozměrů elips a hyperbol.

Elipsa

Hlavní osa elipsy je její nejdelší průměr, přímka, která prochází středem a oběma ohnisky, její konce jsou v nejširších bodech útvaru. Poloměrná osa je polovinou hlavní osy a vede tedy od středu přes ohnisko až k okraji elipsy.

S poloměrnou osou {\displaystyle b\,\!} souvisí prostřednictvím excentricity {\displaystyle e\,\!} a polopřímkou {\displaystyle \ell \,\!} takto:

{\displaystyle b=a{\sqrt {1-e^{2}}},\!}{\displaystyle \ell =a(1-e^{2})\,\!}{\displaystyle a\ell =b^{2}\,\!}.

Parabolu lze získat jako limitu posloupnosti elips, kde jedno ohnisko zůstává pevné, zatímco druhé se může libovolně vzdalovat v jednom směru, přičemž {\displaystyle \ell \,\!} zůstává pevné. Tak {\displaystyle a\,\!} a {\displaystyle b\,\!} směřují k nekonečnu, {\displaystyle a\,\!} rychleji než {\displaystyle b\,\!}.

Poloměrná osa je střední hodnota nejmenší a největší vzdálenosti od jednoho ohniska k bodům na elipse. Nyní uvažujme rovnici v polárních souřadnicích s jedním ohniskem v počátku a druhým na kladné ose x,

{\displaystyle r(1-e\cos \theta )=l\,\!}

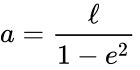
The mean value of {\displaystyle r={\ell \over {1+e}}\,\!} and {\displaystyle r={\ell \over {1-e}}\,\!}, is {\displaystyle a={\ell \over {1-e^{2}}}\,\!}.

Hyperbola

The semi-major axis of a hyperbola is one half of the distance between the two branches; if this is a in the x-direction the equation is:

{\displaystyle {\frac {\left(x-h\right)^{2}}{a^{2}}}-{\frac {\left(y-k\right)^{2}}{b^{2}}}=1}

In terms of the semi-latus rectum and the eccentricity we have

{\displaystyle a={\ell \over e^{2}-1}}

Astronomy

Orbital period

In astrodynamics the orbital period {\displaystyle T\,} of a small body orbiting a central body in a circular or elliptical orbit is:

{\displaystyle T=2\pi {\sqrt {a^{3}/\mu }}}

where:

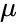
{\displaystyle a\,} je délka poloměrné osy dráhy {\displaystyle \mu } je standardní gravitační parametr

Všimněte si, že pro všechny elipsy s danou poloměrnou osou je oběžná doba stejná bez ohledu na excentricitu.

V astronomii je poloosa spolu s oběžnou dobou jedním z nejdůležitějších prvků oběžné dráhy. U objektů sluneční soustavy souvisí polohová osa s periodou oběhu podle třetího Keplerova zákona (původně odvozeného empiricky),

{\displaystyle T^{2}=a^{3}\,}

kde T je perioda v letech a a je polohová osa v astronomických jednotkách. Ukazuje se, že tento tvar je zjednodušením obecného tvaru pro problém dvou těles, jak jej určil Newton:

{\displaystyle T^{2}={\frac {4\pi ^{2}}{G(M+m)}}a^{3}\,}

kde G je gravitační konstanta a M je hmotnost centrálního tělesa a m je hmotnost obíhajícího tělesa. Obvykle je hmotnost centrálního tělesa o tolik větší než hmotnost obíhajícího tělesa, že m lze zanedbat. Pokud přijmeme tento předpoklad a použijeme typické astronomické jednotky, dostaneme jednodušší tvar, který objevil Kepler.

Pozoruhodné je, že dráha obíhajícího tělesa kolem barycentra i jeho dráha vzhledem k primáru jsou elipsy. Poloměrná osa používaná v astronomii je vždy vzdálenost mezi primárním a sekundárním tělesem; parametry oběhu planet se tedy udávají v heliocentrickém vyjádření. Rozdíl mezi primocentrickými a „absolutními“ drahami lze nejlépe ilustrovat na příkladu soustavy Země-Měsíc. Poměr hmotností je v tomto případě 81,30059. Charakteristická vzdálenost Země-Měsíc, poloosa geocentrické dráhy Měsíce, je 384 400 km. Naproti tomu barycentrická dráha Měsíce má poloosu 379 700 km, přičemž rozdíl 4 700 km připadá na protiběžnou dráhu Země. Průměrná rychlost barycentrické dráhy Měsíce je 1,010 km/s, zatímco průměrná rychlost Země je 0,012 km/s. Součet těchto rychlostí dává geocentrickou průměrnou oběžnou rychlost Měsíce, 1,022 km/s; stejnou hodnotu lze získat, uvažujeme-li pouze hodnotu geocentrické poloosy.

Průměrná vzdálenost

Často se říká, že poloosa je „průměrná“ vzdálenost mezi primárem (ohniskem elipsy) a obíhajícím tělesem. To není zcela přesné, protože záleží na tom, nad čím se průměr bere.

  • průměrováním vzdálenosti nad excentrickou anomálií (q.v.) skutečně získáme poloosu.
  • průměrování přes skutečnou anomálii (skutečný orbitální úhel měřený v ohnisku) vede kupodivu k poloměrné ose {\displaystyle b=a{\sqrt {1-e^{2}}},\!}.
  • průměrováním přes střední anomálii (část oběžné periody, která uplynula od pericentra, vyjádřená jako úhel) nakonec získáme časový průměr (což pro laiky obvykle znamená „průměr“): {\displaystyle a(1+{\frac {e^{2}}{2}})\,\!}.

Časový průměr inverzního poloměru, {\displaystyle r^{-1}\,\!}, je {\displaystyle a^{-1}\,\!}.

Energie; výpočet poloměrné osy ze stavových vektorů

V astrodynamice lze poloměrnou osu {\displaystyle a\,} vypočítat ze stavových vektorů orbitalu:

{\displaystyle a={-\mu \over {2\epsilon }}\,} for an elliptical orbit and {\displaystyle a={\mu \over {2\epsilon }}\,} for a hyperbolic trajectory

and

{\displaystyle \epsilon ={v^{2} \over {2}}-{\mu \over \left|\mathbf {r} \right|}} (specific orbital energy)

and

{\displaystyle \mu =GM\,} (standard gravitational parameter),

where:

  • {\displaystyle v\,} is orbital velocity from velocity vector of an orbiting object,
  • {\displaystyle \mathbf {r} \,} is cartesian position vector of an orbiting object in coordinates of a reference frame with respect to which the elements of the orbit are to be calculated (e.g. geocentrická rovníková pro dráhu kolem Země nebo heliocentrická ekliptikální pro dráhu kolem Slunce),
  • {\displaystyle G\,} je gravitační konstanta,
  • {\displaystyle M\,} hmotnost centrálního tělesa.

Všimněte si, že pro dané centrální těleso a celkovou specifickou energii je poloosa vždy stejná bez ohledu na excentricitu. A naopak, pro dané centrální těleso a poloosu je celková měrná energie vždy stejná.

Příklad

Mezinárodní vesmírná stanice má oběžnou dobu 91,74 minuty, tudíž poloosa je 6738 km . Každá další minuta odpovídá cca 50 km navíc: 300 km délky oběžné dráhy navíc trvá 40 sekund, nižší rychlost představuje dalších 20 sekund.

Napsat komentář

Vaše e-mailová adresa nebude zveřejněna. Vyžadované informace jsou označeny *