Projekce

Projekce

Teď, když jsme si popsali pojem redukce dimenze a některé aplikace SVD a analýzy hlavních komponent, se zaměříme na další podrobnosti týkající se matematiky, která za nimi stojí. Začneme projekcemi. Projekce je pojem lineární algebry, který nám pomáhá porozumět mnoha matematickým operacím, které provádíme s vysokodimenzionálními daty. Podrobnější informace o projekcích najdete v knize o lineární algebře. Zde vám poskytneme stručný přehled a poté uvedeme několik příkladů souvisejících s analýzou dat.

Pro přehled si připomeňme, že projekce minimalizují vzdálenost mezi body a podprostorem.

Na obrázku výše ukazuje bod nahoře na bod v prostoru. V tomto konkrétním obrázku je prostor dvourozměrný, ale měli bychom uvažovat abstraktně. Prostor je reprezentován kartézskou rovinou a přímka, na které stojí človíček, je podprostorem bodů. Projekcí do tohoto podprostoru je místo, které je nejblíže původnímu bodu. Geometrie nám říká, že tento nejbližší bod najdeme tak, že z bodu do prostoru pustíme kolmici (tečkovanou čáru). Človíček stojí na projekci. Množství, které musel tento človíček ujít od počátku k novému promítanému bodu, se označuje jako souřadnice.

Pro vysvětlení promítání budeme používat standardní zápis maticové algebry pro body: je bod v -rozměrném prostoru a je menší podprostor.

Jednoduchý příklad s N=2

Pokud necháme . Můžeme jej vykreslit takto:

mypar (1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)text(2,3," Y",pos=4,cex=3)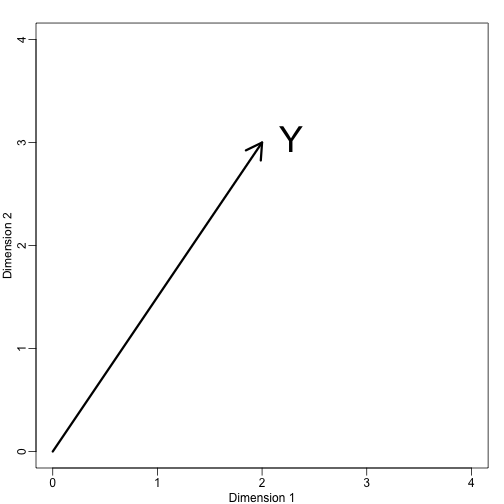

Můžeme ihned definovat souřadnicový systém promítnutím tohoto vektoru do prostoru definovaného: (osa x) a (osa y). Projekce do podprostoru definovaného těmito body jsou 2 a 3:

Řekneme, že a jsou souřadnice a že jsou základny.

Nyní definujme nový podprostor. Červená čára v grafu níže je podprostor definovaný body splňujícími s . Projekce na je nejbližší bod na . Potřebujeme tedy najít takovou, která minimalizuje vzdálenost mezi a . V lineární algebře se učíme, že rozdíl mezi těmito body je ortogonální k prostoru, takže:

z toho vyplývá, že:

a:

Tady tečka představuje bodový součin: .

Následující kód v R potvrzuje, že tato rovnice funguje:

mypar(1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)abline(0,0.5,col="red",lwd=3) #if x=2c and y=c then slope is 0.5 (y=0.5x)text(2,3," Y",pos=4,cex=3)y=c(2,3)x=c(2,1)cc = crossprod(x,y)/crossprod(x)segments(x*cc,x*cc,y,y,lty=2)text(x*cc,x*cc,expression(hat(Y)),pos=4,cex=3)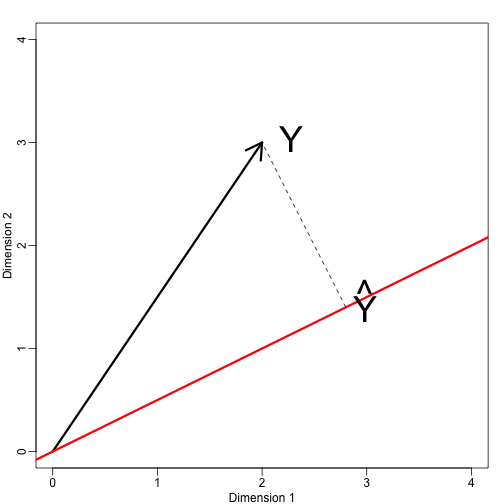

Všimněte si, že pokud bylo takové, že , pak je prostě a prostor se nemění. Toto zjednodušení je jedním z důvodů, proč máme rádi ortogonální matice.

Příklad: V tomto prostoru mají všechny složky vektorů stejné číslo, takže si tento prostor můžeme představit jako prostor reprezentující konstanty: v projekci bude mít každá dimenze stejnou hodnotu. Co tedy minimalizuje vzdálenost mezi a ?

Když hovoříme o problémech, jako je tento, někdy používáme dvourozměrné obrázky, jako je ten výše uvedený. Jednoduše abstrahujeme a považujeme bod v a za podprostor definovaný menším počtem hodnot, v tomto případě jen jednou: .

Vrátíme-li se k naší otázce, víme, že projekce je:

což je v tomto případě průměr:

Tady by také bylo stejně snadné použít výpočet:

Příklad: Regrese je také projekce

Uveďme si o něco složitější příklad. Jednoduchou lineární regresi lze také vysvětlit pomocí projekcí. Naše data (nebudeme již používat zápis) jsou opět vektor a náš model předpovídá pomocí přímky . We want to find the and that minimize the distance between and the space defined by:

with:

Our matrix is and any point in can be written as .

The equation for the multidimensional version of orthogonal projection is:

which we have seen before and gives us:

And the projection to is therefore: