En nuestra discusión sobre el intervalo de confianza para \(\mu_{Y}\), utilizamos la fórmula para investigar qué factores afectan a la anchura del intervalo de confianza. No hay necesidad de hacerlo de nuevo. Como las fórmulas son tan similares, resulta que los factores que afectan a la anchura del intervalo de predicción son idénticos a los factores que afectan a la anchura del intervalo de confianza.
Investiguemos, en cambio, la fórmula del intervalo de predicción para \(y_{new}\):
(\hat{y}_h \pm t_{(1-\alpha/2, n-2)} \t{MSE \t} \t} \t( 1+dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{{suma(x_i-\bar{x})^2}{directo)})
para ver cómo se compara con la fórmula del intervalo de confianza para \(\mu_{Y}):
(\hat{y}_h \pm t_(1-\alpha/2, n-2)} \times \sqrt{MSE \left(\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{{suma(x_i-\bar{x})^2}{derecha)})
Obsérvese que la única diferencia en las fórmulas es que el error estándar de la predicción para \(y_{nuevo}) tiene un término MSE extra que el error estándar del ajuste para \(\mu_{Y}} no tiene.
Tratemos de entender el intervalo de predicción para ver qué causa el término MSE extra. Al hacerlo, vamos a empezar con un problema más fácil primero. Pensemos en cómo podríamos predecir una nueva respuesta \ (y_{new}) en un determinado \ (x_{h}) si se conociera la media de las respuestas \ (\mu_{Y}) en \ (x_{h}). Es decir, supongamos que se conoce que la media de la mortalidad por cáncer de piel en \(x_{h} = 40^{o}} N es de 150 muertes por millón (con varianza 400). ¿Cuál es la mortalidad por cáncer de piel predicha en Columbus, Ohio?
Dado que se conocen \(\mu_{Y} = 150 \) y \( \sigma^{2} = 400\), podemos aprovechar la «regla empírica», que establece, entre otras cosas, que el 95% de las medidas de los datos distribuidos normalmente están dentro de 2 desviaciones estándar de la media. Es decir, dice que el 95% de las medidas se encuentran en el intervalo comprendido entre:
(\mu_{Y}- 2\sigma\) y \(\mu_{Y}+ 2\sigma\).
Aplicando la regla del 95% a nuestro ejemplo con \(u_{Y} = 150\) y \(\sigma= 20\):
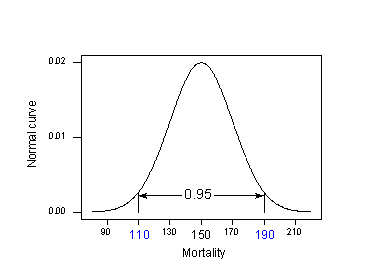
El 95% de las tasas de mortalidad por cáncer de piel de los lugares situados a 40 grados de latitud norte se encuentran en el intervalo comprendido entre:
150 – 2(20) = 110 y 150 + 2(20) = 190.
Es decir, si alguien quisiera conocer la tasa de mortalidad por cáncer de piel de una localidad a 40 grados norte, nuestra mejor estimación estaría entre 110 y 190 muertes por cada 10 millones. El problema es que nuestro cálculo utilizó \(\mu_{Y}\) y \(\sigma\), valores poblacionales que normalmente desconocemos. La realidad se impone:
- La media \(\mu_{Y}) normalmente no se conoce. Lo lógico es estimarla con la respuesta predicha \(\hat{y}\). El coste de utilizar \hat{y} para estimar \mu_{Y} es la varianza de \hat{y}. Es decir, diferentes muestras arrojarían diferentes predicciones \(\hat{y}\), por lo que tenemos que tener en cuenta esta varianza de \(\hat{y}\).
- La varianza \( \sigma^{2}\) normalmente no se conoce. Lo lógico es estimarla con el MSE.
Debido a que tenemos que estimar estas cantidades desconocidas, la variación en la predicción de una nueva respuesta depende de dos componentes:
- la variación debida a la estimación de la media \(\mu_{Y}\) con \(\hat{y}_h) , que denotamos «\(\sigma^2(\hat{Y}_h)\N».)» (Obsérvese que la estimación de esta cantidad no es más que el cuadrado del error estándar del ajuste que aparece en la fórmula del intervalo de confianza.)
- la variación en las respuestas y, que denotamos como «\(\sigma^2\).» (Obsérvese que la cantidad se estima, como es habitual, con el error cuadrático medio MSE.)
- Debido a que el intervalo de predicción tiene el término MSE extra, un intervalo de confianza para \(u_{Y}}) en \(x_{h}) siempre será más estrecho que el correspondiente intervalo de predicción para \(y_{new}} en \(x_{h}).
- Calculando el intervalo en la media de la muestra de los valores del predictor \(\left(x_{h} = \bar{x}\right)\Ny aumentando el tamaño de la muestra n, el error estándar del intervalo de confianza puede acercarse a 0. Debido a que el intervalo de predicción tiene el término extra MSE, el error estándar del intervalo de predicción no puede acercarse a 0.
Sumando los dos componentes de la varianza, obtenemos:
(\sigma^2+\sigma^2(\hat{Y}_h)
que se estima mediante:
(MSE+MSE \left( \dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \right) =MSE\left( 1+\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \N – derecha) \N -)
¿Reconoces esta cantidad? Es simplemente la varianza de la predicción que aparece en la fórmula del intervalo de predicción \(y_{new})!
Volvamos a comparar los dos intervalos:
Intervalo de confianza para \(\mu_{Y}\colon \hat{y}_h \pm t_(1-\alpha/2, n-2)} \m veces \qrt{MSE \m veces \frac( \frac{1}{n} + \frac{(x_h-\bar{x})^2}{{suma(x_i-\bar{x})^2}{directo)})
Intervalo de predicción para (y_{new}}colon \hat{y}_h pm t_(1-\alpha/2, n-2)} \más veces \qrt{MSE \left( 1+\frac{1}{n} + \frac{(x_h-\bar{x})^2}{suma(x_i-\bar{x})^2}{directo)})
¿Cuáles son las implicaciones prácticas de la diferencia de las dos fórmulas?
La primera implicación se ve más fácilmente estudiando el siguiente gráfico para nuestro ejemplo de mortalidad por cáncer de piel:
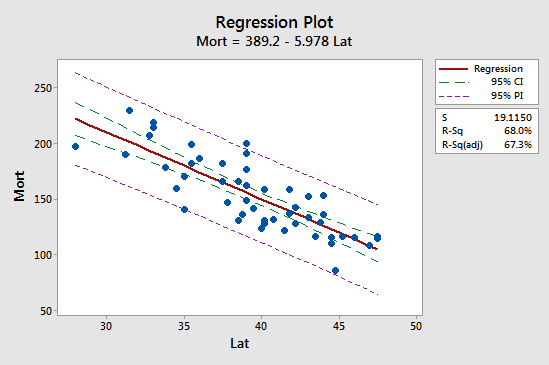
Observe que el intervalo de predicción (IP del 95%, en morado) es siempre más amplio que el intervalo de confianza (IC del 95%, en verde). Además, ambos intervalos son más estrechos en la media de los valores predictores (alrededor de 39,5).