En esta sección, aprenderemos a encontrar la(s) raíz(es) de una ecuación cuadrática. Las raíces también se llaman interceptos x o ceros. Una función cuadrática se representa gráficamente por una parábola con el vértice situado en el origen, por debajo del eje x o por encima del eje x. Por tanto, una función cuadrática puede tener una, dos o cero raíces.
Cuando se nos pide que resolvamos una ecuación cuadrática, en realidad se nos está pidiendo que encontremos las raíces. Ya hemos visto que completar el cuadrado es un método útil para resolver ecuaciones cuadráticas. Este método se puede utilizar para derivar la fórmula cuadrática, que se utiliza para resolver ecuaciones cuadráticas. De hecho, las raíces de la función,
f (x) = ax2 + bx + c
están dadas por la fórmula cuadrática. Las raíces de una función son los intersticios de x. Por definición, la coordenada y de los puntos situados en el eje x es cero. Por lo tanto, para encontrar las raíces de una función cuadrática, ponemos f (x) = 0, y resolvemos la ecuación,
ax2 + bx + c = 0.
We can do this by completing the square as,
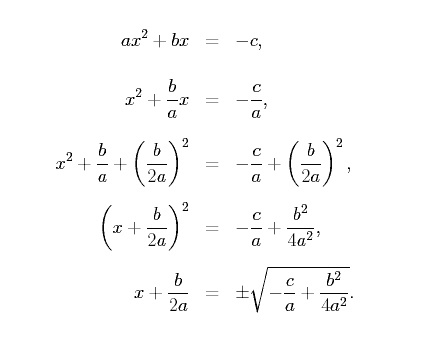
Solving for x and simplifying we have,
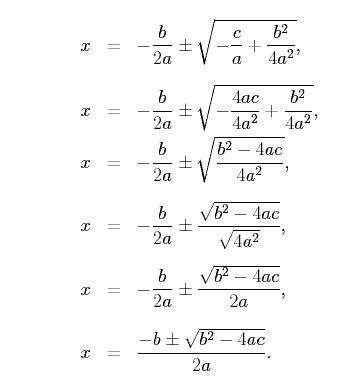
Thus, the roots of a quadratic function are given by,
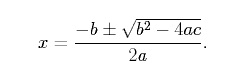
This formula is called the quadratic formula, and its derivation is included so that you can see where it comes from. We call the term b2 −4ac the discriminant. The discriminant is important because it tells you how many roots a quadratic function has. Specifically, if
1. b2 −4ac < 0 There are no real roots.
2. b2 −4ac = 0 There is one real root.
3. b2 −4ac > 0 There are two real roots.
We will examine each case individually.
Caso 1: Sin raíces reales
Si el discriminante de una función cuadrática es menor que cero, esa función no tiene raíces reales, y la parábola que representa no interseca el eje x. Como la fórmula cuadrática requiere tomar la raíz cuadrada del discriminante, un discriminante negativo crea un problema porque la raíz cuadrada de un número negativo no está definida sobre la recta real. Un ejemplo de función cuadrática sin raíces reales viene dado por,
f(x) = x2 – 3x + 4.
Nota que el discriminante de f(x) es negativo,
b2 -4ac = (-3)2- 4 – 1 – 4 = 9 – 16 = -7.
Esta función se representa gráficamente mediante una parábola que se abre hacia arriba cuyo vértice se encuentra por encima del eje x. Por tanto, la gráfica nunca puede intersecar el eje x y no tiene raíces, como se muestra a continuación,
Caso 2: Una raíz real
Si el discriminante de una función cuadrática es igual a cero, dicha función tiene exactamente una raíz real y cruza el eje x en un único punto. Para ver esto, ponemos b2 -4ac = 0 en la fórmula cuadrática para obtener,
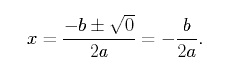
Observa que 
es la coordenada x del vértice de una parábola. Así, una parábola tiene exactamente una raíz real cuando el vértice de la parábola se encuentra justo en el eje x. El ejemplo más sencillo de una función cuadrática que tiene una sola raíz real es,
y = x2,
donde la raíz real es x = 0.
Otro ejemplo de función cuadrática con una raíz real viene dado por,
f(x) = -4×2 + 12x – 9.
Nota que el discriminante de f(x) es cero,
b2 -4ac = (12)2- 4 – -4 -9 = 144 – 144 = 0.
Esta función se representa gráficamente por una parábola que se abre hacia abajo y tiene el vértice (3/2, 0), situado en el eje x. Thus, the graph intersects the x-axis at exactly one point (i.e. has one root) as shown below,
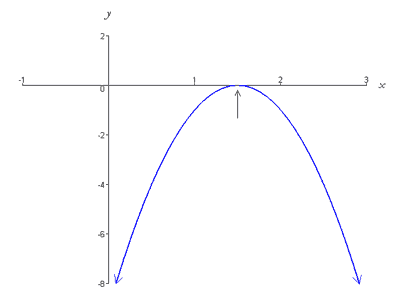
Case 3: Two Real Roots
If the discriminant of a quadratic function is greater than zero, that function has two real roots (x-intercepts). Taking the square root of a positive real number is well defined, and the two roots are given by,
An example of a quadratic function with two real roots is given by,
f(x) = 2×2− 11x + 5.
Notice that the discriminant of f(x) is greater than zero,