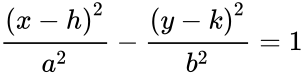Eje semimayor | Space Wiki | Organic Articles

File:Semimajoraxis.png

El semieje mayor de una elipse

En geometría, el término semieje mayor (también eje semimayor) se utiliza para describir las dimensiones de las elipses e hipérbolas.

Elipse
Hyperbola
Astronomy
Orbital period
Distancia media
Energía; cálculo del semieje mayor a partir de los vectores de estado
Ejemplo

Elipse

El eje mayor de una elipse es su diámetro más largo, una línea que pasa por el centro y ambos focos, estando sus extremos en los puntos más anchos de la forma. El semieje mayor es la mitad del eje mayor y, por tanto, va desde el centro, pasando por un foco, hasta el borde de la elipse.

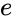
Se relaciona con el semieje menor ${{displaystyle b,\}$ a través de la excentricidad ${{displaystyle e,\}$ .} y el semilato recto ${{displaystyle \ell \}$ ., de la siguiente manera:

${displaystyle b=a{sqrt {1-e^{2}},\}$ ${displaystyle \ell =a(1-e^{2})\}$ ${displaystyle a\ell =b^{2}\},}$ .

Una parábola puede obtenerse como el límite de una secuencia de elipses en las que se mantiene fijo un foco mientras se permite que el otro se aleje arbitrariamente en una dirección, manteniendo ${{displaystyle \ell \\}$ fijo. Así, ${displaystyle a,\!}$ y ${displaystyle b,\!}$ tienden al infinito, ${displaystyle a,\!}$ } más rápido que ${displaystyle b,\!}$ .

El semieje mayor es el valor medio de las distancias menor y mayor de un foco a los puntos de la elipse. Consideremos ahora la ecuación en coordenadas polares, con un foco en el origen y el otro en el eje x positivo,

${{displaystyle r(1-e\cos \theta )=l,\}.}$

The mean value of $r={\ell \over {1+e}}\,\!$ and $r={\ell \over {1-e}}\,\!$ , is $a={\ell \over {1-e^{2}}}\,\!$ .

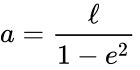
Hyperbola

The semi-major axis of a hyperbola is one half of the distance between the two branches; if this is a in the x-direction the equation is:

${\frac {\left(x-h\right)^{2}}{a^{2}}}-{\frac {\left(y-k\right)^{2}}{b^{2}}}=1$

In terms of the semi-latus rectum and the eccentricity we have

$a={\ell \over e^{2}-1}$

Astronomy

Orbital period

In astrodynamics the orbital period 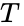$T\,$ of a small body orbiting a central body in a circular or elliptical orbit is:

$T=2\pi {\sqrt {a^{3}/\mu }}$

where:

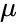
${displaystyle a\\}$ es la longitud del semieje mayor de la órbita ${displaystyle \mu }$ es el parámetro gravitatorio estándar

Nota que para todas las elipses con un semieje mayor dado, el periodo orbital es el mismo, independientemente de la excentricidad.

En astronomía, el semieje mayor es uno de los elementos orbitales más importantes de una órbita, junto con su período orbital. Para los objetos del sistema solar, el semieje mayor se relaciona con el periodo de la órbita mediante la tercera ley de Kepler (originalmente derivada empíricamente),

$T^{2}=a^{3},$

donde T es el periodo en años, y a es el semieje mayor en unidades astronómicas. Esta forma resulta ser una simplificación de la forma general para el problema de los dos cuerpos, determinada por Newton:

${{displaystyle T^{2}={\frac {4\pi ^{2}}{G(M+m)}}a^{3},}$

donde G es la constante gravitatoria, y M es la masa del cuerpo central, y m es la masa del cuerpo en órbita. Normalmente, la masa del cuerpo central es mucho mayor que la del cuerpo en órbita, por lo que se puede ignorar m. Si se hace esta suposición y se utilizan las unidades típicas de la astronomía, se obtiene la forma más sencilla que descubrió Kepler.

Notablemente, la trayectoria del cuerpo en órbita alrededor del baricentro y su trayectoria relativa a su primario son ambas elipses. El semieje mayor utilizado en astronomía es siempre la distancia entre el primario y el secundario; así, los parámetros orbitales de los planetas se dan en términos heliocéntricos. La diferencia entre las órbitas primocéntricas y las «absolutas» puede ilustrarse mejor observando el sistema Tierra-Luna. La relación de masas en este caso es de 81,30059. La distancia característica Tierra-Luna, el semieje mayor de la órbita lunar geocéntrica, es de 384.400 km. La órbita lunar baricéntrica, en cambio, tiene un semieje mayor de 379.700 km, y la contraórbita de la Tierra ocupa la diferencia, 4.700 km. La velocidad orbital baricéntrica media de la Luna es de 1,010 km/s, mientras que la de la Tierra es de 0,012 km/s. La suma de estas velocidades da la velocidad orbital media lunar geocéntrica, 1,022 km/s; el mismo valor puede obtenerse considerando sólo el valor del semieje mayor geocéntrico.

Distancia media

A menudo se dice que el semieje mayor es la distancia «media» entre el primario (el foco de la elipse) y el cuerpo en órbita. Esto no es del todo exacto, ya que depende sobre qué se tome la media.

Promediando la distancia sobre la anomalía excéntrica (q.v.) se obtiene efectivamente el semieje mayor.
Promediar sobre la verdadera anomalía (el verdadero ángulo orbital, medido en el foco) da como resultado, curiosamente, el semieje menor ${{displaystyle b=a{{sqrt {1-e^{2}}},\}.}$ .
Promediando sobre la anomalía media (la fracción del período orbital que ha transcurrido desde el pericentro, expresada en forma de ángulo), finalmente, se obtiene la media temporal (que es lo que suele significar «media» para los profanos): ${{displaystyle a(1+{\\frac {e^{2}}{2}})}{{\i}$ .

La media temporal de la inversa del radio, ${{displaystyle r^{-1},\!}$ , es ${displaystyle a^{-1},\!}$ .

Energía; cálculo del semieje mayor a partir de los vectores de estado

En astrodinámica el semieje mayor ${displaystyle a,}$ puede calcularse a partir de los vectores de estado orbitales:

$a={-\mu \over {2\epsilon }}\,$ for an elliptical orbit and $a={\mu \over {2\epsilon }}\,$ for a hyperbolic trajectory

and

$\epsilon ={v^{2} \over {2}}-{\mu \over \left|\mathbf {r} \right|}$ (specific orbital energy)

and

$\mu =GM\,$ (standard gravitational parameter),

where:

$v\,$ is orbital velocity from velocity vector of an orbiting object,
$\mathbf {r} \,$ is cartesian position vector of an orbiting object in coordinates of a reference frame with respect to which the elements of the orbit are to be calculated (e.g. geocéntrico ecuatorial para una órbita alrededor de la Tierra, o heliocéntrico eclíptico para una órbita alrededor del Sol),
${displaystyle G\,}$ es la constante gravitatoria,
${displaystyle M\,}$ la masa del cuerpo central.

Nótese que para un cuerpo central y una energía específica total dados, el semieje mayor es siempre el mismo, independientemente de la excentricidad. A la inversa, para un cuerpo central y un eje semimayor dados, la energía específica total es siempre la misma.

Ejemplo

La Estación Espacial Internacional tiene un periodo orbital de 91,74 minutos, por lo que el eje semimayor es de 6738 km . Cada minuto más corresponde a unos 50 km más: los 300 km adicionales de longitud de la órbita requieren 40 segundos, la menor velocidad supone 20 segundos adicionales.