Una función de producción Cobb-Douglas modela la relación entre la producción y los insumos de producción (factores). Se utiliza para calcular las relaciones entre los insumos para una producción eficiente y para estimar el cambio tecnológico en los métodos de producción. La forma general de una función de producción Cobb-Douglas para un conjunto de \(n\) insumos es \(Y), donde \(Y) representa la producción, \(x_{i}\) el insumo \(i\), y \(\gamma\) y \(\alpha_{i}) son parámetros que determinan la eficiencia global de la producción y la capacidad de respuesta de la producción a los cambios en las cantidades de entrada. La aplicación de esta forma funcional en la medición de la producción se debe al matemático Charles Cobb y al economista Paul Douglas, que la utilizaron para considerar la importancia relativa de los dos factores de entrada, el trabajo y el capital, en la producción manufacturera de EE.UU. durante el período de 1899 a 1922. En su modelo original, Cobb y Douglas restringen los parámetros de elasticidad de la producción \(\alpha_{1}) y \(\alpha_{2}) al intervalo \(\alpha_{i}en\\a la izquierda(0,1\a la derecha)\a la suma de uno, lo que implica rendimientos constantes a escala. La función es, por tanto, donde \(x_{1}\}) y \(x_{2}\} representan el trabajo y el capital, respectivamente. Tomando el logaritmo natural de ambos lados de la ecuación se obtiene que para los datos de producción, trabajo y capital, los parámetros \(\gamma\) y \(\alpha_{1}\) pueden ser estimados utilizando mínimos cuadrados ordinarios. Sobre la base de sus datos, Cobb y Douglas encuentran un valor de 0,75 para \\N(\alpha_{1}), lo que implica que la mano de obra representó tres cuartas partes del valor de la producción manufacturera de EE.UU. (el capital representa la cuarta parte restante) durante el período estudiado. Su estimación del parámetro de eficiencia \(\gamma\) es de 1,01, que, al ser mayor que 1, refleja los efectos positivos de las fuerzas inobservables en la producción a través de la combinación de trabajo y capital.
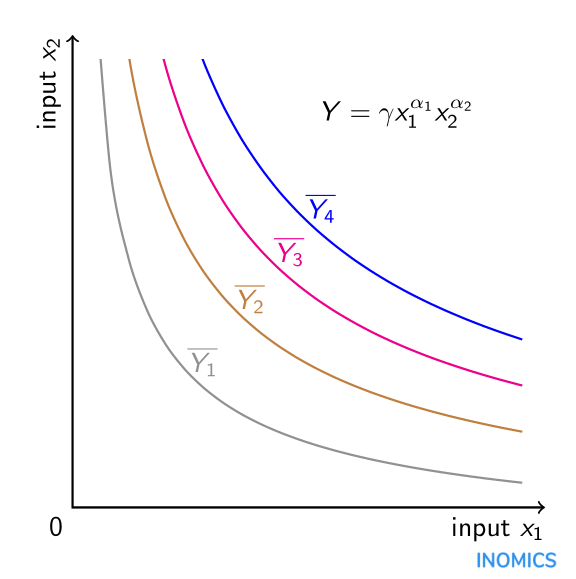
La naturaleza multiplicativa de una función de producción Cobb-Douglas, asumiendo valores positivos para \(\alpha_{i}\), significa que los inputs son complementos en la producción. En el modelo estándar de trabajo y capital, el aumento de la cantidad de capital aumenta la producción no sólo directamente, sino también indirectamente a través de su impacto en la productividad del trabajo. Matemáticamente, la derivada parcial cruzada de la producción \(Y\) con respecto al trabajo \(x_{1}\) y al capital \(x_{2}\) es positiva. Además, debido a la suposición de que \(\alpha_{i}en la izquierda(0,1\\\a la derecha)\a), las derivadas parciales de segundo orden de la producción con respecto al trabajo y con respecto al capital son ambas negativas, lo que implica rendimientos marginales decrecientes para cada insumo por sí solo. El simple hecho de añadir más mano de obra o más capital (pero no ambos) al proceso de producción aumenta la producción, aunque a un ritmo decreciente. Además, la elasticidad de sustitución entre los insumos es constante e igual a uno debido a la forma funcional. Una función de producción Cobb-Douglas de dos insumos puede representarse gráficamente en forma de isocuantas: combinaciones de ambos insumos para las que la producción es constante. Hay cuatro isocuantas de este tipo en el gráfico para los niveles de producción (constantes) \ ~ sobre la línea de Y_{1}}, \ ~ sobre la línea de Y_{2}}, \ ~ sobre la línea de Y_{3}} y \ ~ sobre la línea de Y_{4}}. Cuanto más lejos esté la isocuanta del origen, mayor será el nivel de producción \(\overline{Y_{4}}>overline{Y_{3}}>overline{Y_{2}}>overline{Y_{1}}). Qué combinación precisa de los insumos \(x_{1}} y \(x_{2}} es óptima para la producción viene determinada por el presupuesto del que dispone el productor, así como por la relación de costes entre el insumo \(x_{2}} y el insumo \(x_{1}}, que puede incluirse en el gráfico en forma de línea de isocoste (véase el artículo sobre la elasticidad de sustitución).
Los propios Cobb y Douglas reconocieron que su función de producción no se apoya en sólidos fundamentos teóricos, ni debe entenderse como una ley de producción; simplemente representa una aproximación estadística de las relaciones observadas entre los inputs de producción y el output. No obstante, sus sencillas propiedades matemáticas resultan atractivas para los economistas y han hecho que se convierta en un estándar de la teoría microeconómica durante el último siglo.
Lectura adicional:
Para los antecedentes y una visión general de las principales propiedades de las funciones de producción Cobb-Douglas, véanse en particular las secciones 6, 7 y 8 del artículo original de Cobb y Douglas, «A Theory of Production» (The American Economic Review, 1928).
Es bueno saberlo:
La forma funcional Cobb-Douglas no sólo se utiliza en la teoría de la producción, sino que también se ha convertido en estándar en la teoría microeconómica del consumidor, donde se aplica como función de utilidad, donde \(Y\) se convierte en \(U\) para la utilidad. Los \(x_{i}) representan entonces los artículos de consumo y, cuando la función de utilidad se maximiza sujeta a una restricción presupuestaria, los valores de \(\_alfa_{i}) indican cómo el individuo distribuirá óptimamente el presupuesto entre los artículos.