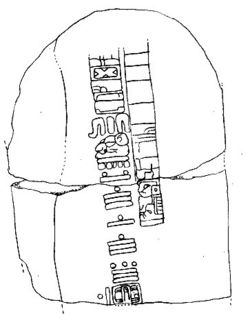
Estela de Tres Zapotes – 31 a.C.
La Cuenta Larga, de la que no conocemos el nombre maya, se considera comúnmente la cuenta lineal de los días de los mayas. En realidad se trata de otro ciclo, pero su gran longitud de al menos 5126 años hace que sea esencialmente una cuenta lineal a través de toda la historia maya. La primera fecha conocida de la cuenta larga, tallada en el año 31 a.C., se encontró en el sitio olmeca de Tres Zapotes. La primera cuenta larga maya conocida se registró en el año 32 d.C. en el sitio de Chiapa de Corzo, en los Altos de Chiapas, México. Al igual que el calendario cristiano, la cuenta larga tiene una fecha de inicio: la nuestra es el 1 de enero de 0 d.C., y la suya (según nuestros cálculos) es el 11 de agosto de 3114 a.C. Pero a diferencia del nuestro, el suyo también tiene una fecha aparente de finalización, el 21 de diciembre de 2012 d.C. La cuenta larga se representa como un sistema de notación de cinco lugares de ciclos ascendentes: kins (días), winals (meses de 20 días), tuns (360 días), k’atuns (20 tuns) y bak’tuns (20 k’atuns). Es importante señalar que la versión de la cuenta larga de un año, el tun, sólo tiene 360 días, no la cuenta solar de 365. Esto significa que la cuenta larga difiere de la Haab en cinco días cada año, lo que la convierte en un ciclo completamente único y separado.

Las cinco posiciones de la cuenta larga
El mayor de los cinco ciclos de la cuenta larga, el bak’tun, es un período equivalente a 400 tuns. Mucha gente cree que el ciclo completo de la Cuenta Larga se completa cuando han pasado 13 bak’tuns desde el comienzo de la creación de este universo actual, identificado como la 4ª creación en la «historia de la creación» maya, el Popol Vuh. Esa fecha, actualmente de gran interés para aquellos que anticipan un «fin de los días», ocurrirá el 21 de diciembre de 2012 DC.
To further illustrate how the Long Count moves forward through time, look at the day sequencing around the beginning and end of the cycle:
| 12.19.19.17.19 | 3 Kawak 7 Kumku | August 10, 3114 BC |
| 13.0.0.0.0 | 4 Ahau 8 Kumku | August 11, 3114 BC |
| 0.0.0.0.1 | 5 Imix 9 Kumku | August 12, 3114 BC |
| 12.19.19.17.19 | 3 Kawak 2 Kankin | December 20, 2012 AD |
| 13.0.0.0.0 | 4 Ahau 3 Kankin | December 21, 2012 AD |
| 0.0.0.0.1 | 5 Imix 4 Kankin | December 22, 2012 AD |
It’s important to point out that this is just one possible scenario for how the Long Count functions and flows. Hay otros estudiosos que creen que la cuenta no se restablecería a 0.0.0.1, sino que continuaría con 13 como los bak’tuns, siendo 13.0.0.1, y luego 13.0.0.2, y así sucesivamente hasta el 14º bak’tuns, siendo representado como 1.0.0.0. Lloyd Anderson ha presentado este escenario en su sitio web en www.traditionalhighcultures.com/MayaMath&WorldAges.html . Dado que no tenemos textos que presenten fechas dentro del rango de 400 tun del primer bak’tun, esta cuestión en particular sigue siendo un debate académico.
Otra creencia muy extendida sobre la Cuenta Larga es que el bak’tun de hecho no se reinicia en 13, sino que es más bien otro ciclo de 20 como todos los demás valores de lugar, con la excepción de los meses, o winals. Los winales son 18, y eso se debe probablemente a que el calendario solar maya, el Haab, está dividido en 18 meses de 20 días cada uno. Sir J. Eric Thompson, uno de los mayistas más influyentes que ha estudiado el calendario, estaba convencido de que el ciclo de los baktunes era de 20, no de 13. Explicó su lógica en el siguiente pasaje:
«Siempre he asumido que los bak’tuns estaban agrupados, no en 13, sino en 20, porque la evidencia que apoya un conteo vigesimal de baktuns en el Dresden y en Palenque y Copan es demasiado fuerte para ser anulada. Asumo que en una fecha temprana, cuando la LC fue inventada por primera vez, el período más alto era el baktun y que los baktunes estaban organizados en series reentrantes de 13, pero que un deseo posterior de ampliar el rango de tiempo llevó a la invención del pictun y de períodos aún mayores. Con esa ampliación del tiempo, era imprescindible encajar los baktunes en un recuento vigesimal. En consecuencia, 20 baktunes se convirtieron en el equivalente de un pictun, pero para entonces 4 Ahau 8 Cumku estaba tan fuertemente establecido como el fin de ciclo de una ronda de 13 baktunes que se le siguió dando esa designación, aunque se le contara como el fin de un ciclo de 20 baktunes a efectos de cálculo». (Thompson 1960, p 316)
Thompson’s passage brings up an important fact about the long count that is not often discussed – the fact that the Maya recorded higher cycles above the bak’tun. Here are the first few of the known long count cycles above bak’tun:
| Piktun | 20 Bak’tuns | 8000 tuns | 2,880,000 days |
| Kalabtun | 20 Piktuns | 160,000 tuns | 57,600,000 days |
| Kinichiltun | 20 Kalabtuns | 3,200,000 tuns | 1,152,000,000 days |
| Alautun | 20 Kinichiltuns | 64,000,000 tuns | 23,040,000,000 days |
(It should noted that while these are the names for these cycles that have been used in the literature for almost a century, there is no direct evidence that these were their names in ancient times.)
These higher cycles are not uncommon in the inscriptions. Aparecen varias veces en el Códice Dresde y en las inscripciones talladas y pintadas de Palenque, Copán, Quirigua, Tikal, Yaxchilán y Cobá. La propia existencia de estos ciclos superiores pone en duda la idea de que la Cuenta Larga se reinicia en el 13º bak’tun. Si así fuera, ¿por qué habría entonces necesidad de estos ciclos de orden superior?

El Panel Oeste del Templo de las Inscripciones (dibujo de Linda Schele)
Volviendo a la cuestión de si el lugar del bak’tun corre en un ciclo de 13 o 20 bak’tuns, un ejemplo de Palenque ha sido utilizado durante mucho tiempo para apoyar el argumento de que 20 bak’tuns equivalen a un piktun.
El texto de la Tabla Occidental del Templo de las Inscripciones menciona la fecha del cumpleaños de Pakal y luego cuenta hacia el futuro para llegar a 1 piktun.
El dibujo de la derecha muestra el segmento del texto que se discute aquí (dibujo de Linda Schele). La matemática sólo funciona si 20 bak’tuns equivalen a un piktun. Here’s the progression:
| 9.8.9.13.0 | 8 Ahau 13 Pop | March 24, 603 AD | Pakal’s Birth |
| + | |||
| 10.11.10.5.8 | The text indicates to go this many days into the future | ||
| To arrive at: | |||
| (1.0.0.0.0.8) | 5 Lamat 1 Mol | The text says 1 piktun 8 kins | |
| And then it mentions the calendar round for the date of exactly one piktun: | |||
| (1.0.0.0.0.0) | 10 Ahau 13 Yaxk’in | October 13, 4772 AD | |
One can see how the distance number of 10.11.10.5.8 was chosen very intentionally to get all zeros in the lower order cycles. Si el ciclo bak’tun giraba por 13, entonces la cuenta larga a la que se llegó habría sido 1.7.0.0.0.8, no 1.0.0.0.8.

La Tabla de la Cruz oeste
dibujo de Linda Schele)
En cuanto a por qué estos textos que hablan de Pakal van tan lejos en el futuro, los hechos son pocos y las teorías muchas. ¿Quizás se trata de una declaración sobre la naturaleza eterna de su alma? ¿O una futura reencarnación? Un punto interesante es que la ronda del calendario 5 Lamat 1 Mol es también la fecha de la ascensión de Pakal en el 612 d.C., y el 5 Lamat 1 Mol al que se llega en el pasaje es exactamente 80 rondas del calendario (ciclos de 52 años) más tarde. Dado que Pakal tenía 80 tuns cuando murió, tal vez se trate de una afirmación poética que alude a su gran edad.
Entonces, si tenemos pruebas claras de que el ciclo del bak’tun, al igual que todas las demás posiciones de la cuenta larga, salvo los winals, transcurre en ciclos de 20, ¿por qué hay tanta gente que cree que se reiniciará con la llegada del 13º bak’tun en 2012 d.C.? La respuesta está en la suposición matemática occidental de que si la cuenta larga comenzó en 13 bak’tuns, entonces debe terminar en 13 bak’tuns. Cuando una persona de la cultura occidental se imagina un ciclo, inmediatamente evoca la imagen de un reloj, con una manecilla giratoria que empieza y termina a las 12. ¿Tiene que ser así? Parte de la cuestión radica en suponer que las nociones occidentales modernas y mesoamericanas antiguas de «ciclo» son las mismas.
Hay inscripciones en Palenque, Copan y Quirigua que fechan específicamente eventos ocurridos antes de la era actual. Todas ellas afirman que ocurrieron dentro del 12º bak’tun y conducen a 13.0.0.0 4 Ahau 8 Kumku. En Palenque, los textos del Grupo de la Cruz afirman que el 9 de diciembre de 3121 a.C. nació una mujer llamada Muwan Mat. Luego, 754 años después del inicio de la era, el 11 de agosto de 3114 a.C., dio a luz a GI de la Tríada de Palenque el 23 de octubre de 2360 a.C. Estas fechas abarcan la fecha de creación, comenzando en un 12º bak’tun y retomando en un 1º bak’tun. Here are the long counts in sequential order:
| 12.19.13.4.0 | 8 Ahau 18 Sek | December 9, 3120 BC | Birth of Muwan Mat |
| 13.0.0.0.0 | 4 Ahau 8 Kumku | August 11, 3114 BC | Creation Date |
| 1.18.5.3.7 | 13 Kimi 19 Keh | October 23, 2360 BC | Birth of GI |
These dates are given as full long counts, not abbreviated within distance numbers or implied by calendar rounds. While the evidence is compelling, these few texts from Palenque are almost single handedly responsible for convincing western scholars that the long count will once again reset in 2012 AD.
In point of fact, though we have many instances of the Maya recording 13.0.0.0.0 for August 11, 3114 BC, there is only one text known to record the 13.0.0.0.0 date for December 21, 2012 AD. Se encontró en el Monumento 6 de Tortuguero y el texto está roto justo después de que se mencione la fecha, ocultando el evento al que se iba a hacer referencia.
Para los antiguos mayas, el 13 bak’tun terminó al comienzo de la cuarta creación o era del mundo. El Popol Vuh describe las tres creaciones anteriores y los destinos de sus habitantes, pero no proporciona fechas. Los aztecas tenían un concepto muy similar y lo explicaron a los españoles con cierto detalle. Para los aztecas, vivían en la quinta era mundial, no en la cuarta. Mark Van Stone (comunicación personal 2008) plantea la hipótesis de que los aztecas pueden haber contado el colapso de la civilización maya clásica en el siglo IX como el final de la 4ª creación.
Los aztecas proporcionaron longitudes de tiempo para cada una de las eras anteriores y, muy importante, no eran las mismas. Aquí están las cuatro eras aztecas anteriores a la actual:
| The first era | 13 cycles of 52 years for a total of 676 years |
| The second era | 7 cycles of 52 years for a total of 364 years |
| The third era | 6 cycles of 52 years for a total of 312 years |
| The fourth era | 13 cycles of 52 years for a total of 676 years |

The Aztec Calendar Stone (National Antropology Museum, Mexico DF)
If one lumps the 2nd and 3rd era time lengths together, they get another set of 13 x 52 years, just like the 1st and 4th eras. Like the Maya, the Aztec seem to have related the concept of 13 cycles with the completion of an era or world creation. The current era was not given a time length, but was predicted by the Aztecs to be ultimately destroyed by earthquakes. Given the difference in past cycle lengths, one could not safely assume that the current Aztec era will be 13 x 52 years. ¿No se aplica esta misma precaución a la noción maya de duración de la era?
Parte de la solución puede estar en distinguir la diferencia conceptual entre un «ciclo» y una «era». Definitivamente hay ciclos sólidos en todo el calendario maya, su naturaleza entrelazada depende de ellos. El kin, el tun, el winal y el k’atun son todos ciclos estáticos de tiempo. El calendario occidental tiene el mismo tipo de incrementos cíclicos: un día, un año, un siglo, un milenio, etc. Sin embargo, una «era» en el pensamiento occidental rara vez es un incremento exacto de un ciclo calendárico. La Edad de Hierro, el Renacimiento, el Industrialismo… cada uno de ellos fue una «era» diferente en la historia con una duración única. ¿Fue la misma diferencia conceptual que expresaron los mayas cuando escribieron que 13 bak’tuns era el fin de una era?
Hay razones para creer que el número 13 se utilizó como una forma simbólica de decir «finalización». Hay textos en Yaxchilán, Cobá y el Códice Dresde que presentan fechas de cuentas largas en las que muchos ciclos por encima del bak’tun repiten el número 13 como sus coeficientes. El ejemplo de Yaxchilán, en un panel frente al Templo 33, coloca diez 13 sobre una fecha contemporánea:
| 13.13.13.13.13.13.13.13.13.13.13.9.15.13.6.9 | 19 de octubre de 744 d.C. |
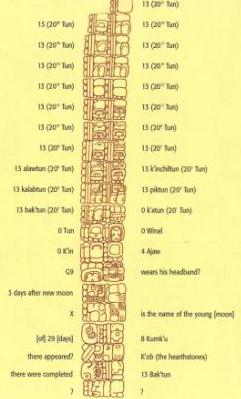
Estela 1 de Coba
(dibujo de Elizabeth Wagner) El ejemplo de Coba, en la Estela 1, sitúa al menos veinte 13 sobre la fecha de creación, 13.0.0.0 11 de agosto de 3314 a.C. Si intentáramos contar realmente todos esos 13 como coeficientes reales, cada uno subiendo una magnitud de 20, ¡la fecha que obtendríamos iría 41.943.040.000.000.000.000.000.000 de años en el pasado! La página 52 del Códice de Dresde también registra una fecha con 13 números consecutivos. Dado que ninguno de estos 13 afecta a los ciclos inferiores, no parece que hayan sido colocados allí para ser calculados realmente. Es probable que sean más bien una declaración simbólica de que han pasado muchos ciclos. Si estos coeficientes de 13 para los piktunes, kalabtunes, kinichiltunes, etc… simbolizan días de hace mucho tiempo, ¿no podrían los 13 bak’tuns estar simbolizando lo mismo?
Entonces, si la idea de que el 13 Bak’tun es el fin de la era actual está en duda, ¿qué debemos pensar de su llegada en 2012 DC? Aunque los textos mayas no dicen nada sobre lo que podría ocurrir en el 13º Bak’tun, sí sabemos que el final de cada bak’tun se consideraba una época de grandes cambios. La revisión de la historia maya antigua proporciona una coroboración general de esa noción.
Los siguientes eventos alrededor del cambio de los últimos cinco bak’tuns no se sugieren como fechas puntuales en las que ocurrieron grandes cambios, sino que se considera el patrón general.
El comienzo del 8º bak’tun (41 d.C.)
Las últimas ciudades olmecas, algunas de las cuales sobrevivieron durante casi 1000 años, fueron abandonadas y nunca volvieron a ser habitadas.
El inicio del 9º bak’tun (435 d.C.)
Comienza la influencia de Teotihuacán en el mundo maya, lo que da lugar a nuevas ciudades, un aluvión de nuevas dinastías y guerras.
El inicio del décimo bak’tun (830 d.C.)
El fin del período Clásico y el abandono aún inexplicable de cientos de ciudades.
El inicio del undécimo bak’tun (1224 d.C.)
El abandono de Chichén Itzá en Yucatán y el surgimiento de Mayapán.
El comienzo del 12º bak’tun (1618 d.C.)
El último gran imperio maya, los itza del lago Petén, enviaron emisarios a los españoles anunciando que estaban dispuestos a aceptar el cambio que traería el cambio de los ciclos.
Fue este último bak’tun, cuando los españoles conquistaron el lago Petén y capturaron al rey Kan Ek, el que proporciona una visión especial de las creencias mayas sobre el cambio de un bak’tun. En el año 1617, Kan Ek envió emisarios a Mérida para informar a los españoles de que el duodécimo bak’tun estaba cerca y que estaban preparados para el cambio que traería. Los españoles interpretaron esto como una voluntad de convertirse al cristianismo y comenzó una carrera entre varios grupos misioneros por el mérito de ser los primeros en convertir finalmente a la poderosa Itza. Con los sacerdotes llegaron los soldados, y el inevitable final. Mientras que los Itza ciertamente no estaban planeando su propia desaparición, tenían razón en que un tiempo de gran cambio estaba sobre ellos.
En conclusión, mientras que es incierto que el 2012 AD marcará el reinicio del ciclo de la cuenta larga, es ciertamente el comienzo del 13º bak’tun. Los antiguos mayas lo habrían considerado un tiempo de grandes cambios. Si cada bak’tun era un momento de gran cambio, entonces el 13º giro debió tener un significado especial, quizás el comienzo de una nueva era en la historia del mundo. El tiempo lo dirá.
El calendario maya seguirá siendo una fuente de gran fascinación, impulsando a la gente a escribir libros y películas sobre la fecha heráldica de 2012. Aunque los ordenadores actuales o los teléfonos móviles o2 tienen calendarios cristianos, la cultura maya seguirá con nosotros incluso después de que se demuestre o no que es obsoleta. Esperamos que hayas disfrutado de este artículo, y por supuesto, si tienes alguna idea o comentario sobre o acerca de la información comentada, no dudes en ponerte en contacto.