Proyecciones
Ahora que hemos descrito el concepto de reducción de dimensión y algunas de las aplicaciones de la SVD y el análisis de componentes principales, nos centramos en más detalles relacionados con las matemáticas que hay detrás. Comenzamos con las proyecciones. Una proyección es un concepto de álgebra lineal que nos ayuda a entender muchas de las operaciones matemáticas que realizamos con datos de alta dimensión. Para más detalles, puedes revisar las proyecciones en un libro de álgebra lineal. Aquí proporcionamos un repaso rápido y luego proporcionamos algunos ejemplos relacionados con el análisis de datos.
Como repaso, recuerde que las proyecciones minimizan la distancia entre los puntos y el subespacio.

En la figura de arriba, el punto en la parte superior está apuntando a un punto en el espacio. En esta viñeta en particular, el espacio es bidimensional, pero debemos pensar en abstracto. El espacio está representado por el plano cartesiano y la línea sobre la que está la personita es un subespacio de puntos. La proyección a este subespacio es el lugar más cercano al punto original. La geometría nos dice que podemos encontrar este punto más cercano dejando caer una línea perpendicular (línea de puntos) desde el punto hasta el espacio. La personita se encuentra en la proyección. La cantidad que esta persona tuvo que caminar desde el origen hasta el nuevo punto proyectado se denomina coordenada.
Para la explicación de las proyecciones, utilizaremos la notación estándar del álgebra matricial para los puntos: es un punto en un espacio -dimensional y es un subespacio más pequeño.
Ejemplo sencillo con N=2
Si dejamos que . Podemos graficarlo así:
mypar (1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)text(2,3," Y",pos=4,cex=3)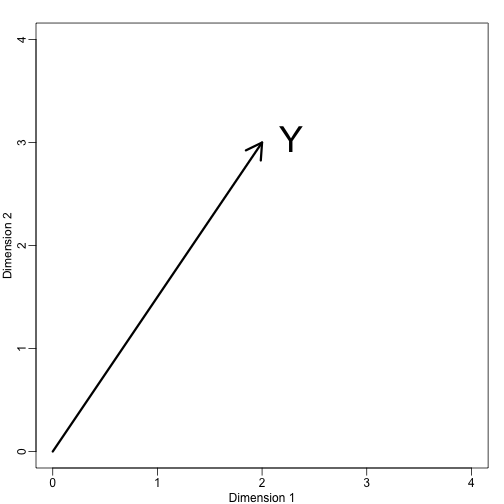
Inmediatamente podemos definir un sistema de coordenadas proyectando este vector al espacio definido por: (el eje x) y (el eje y). Las proyecciones de al subespacio definido por estos puntos son 2 y 3 respectivamente:
Digamos que y son las coordenadas y que son las bases.
Ahora definamos un nuevo subespacio. La línea roja del gráfico de abajo es el subconjunto definido por los puntos que satisfacen con . La proyección de onto es el punto más cercano a . Así que necesitamos encontrar el que minimiza la distancia entre y . En álgebra lineal, aprendemos que la diferencia entre estos puntos es ortogonal al espacio por lo que:
esto implica que:
y:
Aquí el punto representa el producto punto: .
El siguiente código de R confirma que esta ecuación funciona:
mypar(1,1)plot(c(0,4),c(0,4),xlab="Dimension 1",ylab="Dimension 2",type="n")arrows(0,0,2,3,lwd=3)abline(0,0.5,col="red",lwd=3) #if x=2c and y=c then slope is 0.5 (y=0.5x)text(2,3," Y",pos=4,cex=3)y=c(2,3)x=c(2,1)cc = crossprod(x,y)/crossprod(x)segments(x*cc,x*cc,y,y,lty=2)text(x*cc,x*cc,expression(hat(Y)),pos=4,cex=3)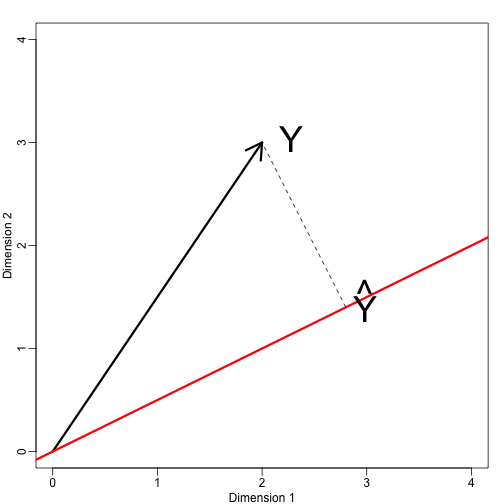
Nótese que si era tal que , entonces es simplemente y el espacio no cambia. Esta simplificación es una de las razones por las que nos gustan las matrices ortogonales.
Ejemplo: La media muestral es una proyección
Dejemos que y es el espacio abarcado por:
En este espacio, todas las componentes de los vectores son el mismo número, por lo que podemos pensar que este espacio representa las constantes: en la proyección cada dimensión será el mismo valor. Entonces, ¿qué es lo que minimiza la distancia entre y?
Cuando hablamos de problemas como éste, a veces utilizamos figuras bidimensionales como la de arriba. Simplemente abstraemos y pensamos en como un punto en y como un subespacio definido por un número menor de valores, en este caso sólo uno: .
Volviendo a nuestra pregunta, sabemos que la proyección es:
que en este caso es la media:
Aquí, también hubiera sido igual de fácil usar el cálculo:
Ejemplo: La regresión también es una proyección
Pongamos un ejemplo algo más complicado. La regresión lineal simple también se puede explicar con proyecciones. Nuestros datos (ya no vamos a usar la notación) vuelven a ser un vector y nuestro modelo predice con una recta . We want to find the and that minimize the distance between and the space defined by:
with:
Our matrix is and any point in can be written as .
The equation for the multidimensional version of orthogonal projection is:
which we have seen before and gives us:
And the projection to is therefore: