Dans notre discussion sur l’intervalle de confiance pour \(\mu_{Y}\), nous avons utilisé la formule pour rechercher quels facteurs affectent la largeur de l’intervalle de confiance. Il n’est pas nécessaire de le faire à nouveau. Les formules étant très similaires, il s’avère que les facteurs affectant la largeur de l’intervalle de prédiction sont identiques aux facteurs affectant la largeur de l’intervalle de confiance.
Etudions plutôt la formule de l’intervalle de prédiction pour \(y_{nouveau}\):
\(\hat{y}_h \pm t_{(1-\alpha/2, n-2)} \times \sqrt{MSE \times \left( 1+\dfrac{1}{n}) + \dfrac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\)
pour voir comment elle se compare à la formule de l’intervalle de confiance pour \(\mu_{Y}\):
\(\hat{y}_h \pm t_{(1-\alpha/2, n-2)} \times \sqrt{MSE \left(\dfrac{1}{n}) + \dfrac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\)
Observez que la seule différence dans les formules est que l’erreur standard de la prédiction pour \(y_{new}\) comporte un terme MSE supplémentaire que l’erreur standard de l’ajustement pour \(\mu_{Y}\) ne comporte pas.
Essayons de comprendre l’intervalle de prédiction pour voir ce qui cause ce terme MSE supplémentaire. Ce faisant, commençons d’abord par un problème plus facile. Pensez à la façon dont nous pourrions prédire une nouvelle réponse \(y_{new}\) à un \(x_{h}\) particulier si la moyenne des réponses \(\mu_{Y}\) à \(x_{h}\) était connue. Autrement dit, supposons que l’on sache que la mortalité moyenne par cancer de la peau à \(x_{h} = 40^{o}\) N est de 150 décès par million (avec une variance de 400) ? Quelle est la mortalité par cancer de la peau prédite à Columbus, Ohio ?
Parce que \(\mu_{Y} = 150 \) et \( \sigma^{2} = 400\) sont connus, nous pouvons tirer parti de la » règle empirique « , qui stipule entre autres que 95 % des mesures de données normalement distribuées se situent à moins de 2 écarts types de la moyenne. Autrement dit, elle dit que 95 % des mesures se trouvent dans l’intervalle pris en sandwich par :
\(\mu_{Y}- 2\sigma\) et \(\mu_{Y}+ 2\sigma\).
Application de la règle des 95% à notre exemple avec \(\mu_{Y} = 150\) et \(\sigma= 20\) :
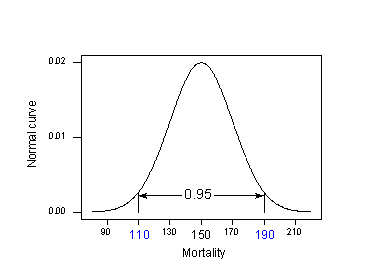
95 % des taux de mortalité par cancer de la peau des localités situées à 40 degrés de latitude nord se trouvent dans l’intervalle pris en sandwich par :
150 – 2(20) = 110 et 150 + 2(20) = 190.
C’est-à-dire que si quelqu’un voulait connaître le taux de mortalité par cancer de la peau pour un endroit situé à 40 degrés de latitude nord, notre meilleure estimation serait quelque part entre 110 et 190 décès pour 10 millions. Le problème est que notre calcul utilise \(\mu_{Y}\) et \(\sigma\), des valeurs de population que nous ne connaîtrions généralement pas. La réalité s’installe :
- La moyenne \(\mu_{Y}\) n’est généralement pas connue. La chose logique à faire est de l’estimer avec la réponse prédite \(\mu_{y}\). Le coût de l’utilisation de \(\hat{y}\) pour estimer \(\mu_{Y}\) est la variance de \(\hat{y}\). C’est-à-dire que différents échantillons donneraient des prédictions différentes \(\hat{y}\), et donc nous devons prendre en compte cette variance de \(\hat{y}\).
- La variance \( \sigma^{2}\) n’est généralement pas connue. La chose logique à faire est de l’estimer avec MSE.
Parce que nous devons estimer ces quantités inconnues, la variation de la prédiction d’une nouvelle réponse dépend de deux composantes :
- la variation due à l’estimation de la moyenne \(\mu_{Y}\) avec \(\hat{y}_h\) , que nous désignons par » \(\sigma^2(\hat{Y}_h)\). » (Notez que l’estimation de cette quantité est juste le carré de l’erreur standard de l’ajustement qui apparaît dans la formule de l’intervalle de confiance.)
- la variation des réponses y, que nous désignons par « \(\sigma^2\). » (Notez que cette quantité est estimée, comme d’habitude, avec l’erreur quadratique moyenne MSE.)
En ajoutant les deux composantes de la variance, nous obtenons :
\(\sigma^2+\sigma^2(\hat{Y}_h)\)
qui est estimée par :
\(MSE+MSE \left( \dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \right) =MSE\left( 1+\dfrac{1}{n} + \dfrac{(x_h-\bar{x})^2}{\sum_{i=1}^{n}(x_i-\bar{x})^2} \N- droite) \N-)
Vous reconnaissez cette quantité ? C’est tout simplement la variance de la prédiction qui apparaît dans la formule de l’intervalle de prédiction \(y_{nouveau}\)!
Comparons à nouveau les deux intervalles:
Intervalle de confiance pour \(\mu_{Y}\colon \hat{y}_h \pm t_{(1-\alpha/2, n-2)}. \times \sqrt{MSE \times \left( \frac{1}{n}) + \frac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\)
Intervalle de prédiction pour \(y_{new}\colon \hat{y}_h \pm t_{(1-\alpha/2, n-2)} \times \sqrt{MSE \left( 1+\frac{1}{n}) + \frac{(x_h-\bar{x})^2}{\sum(x_i-\bar{x})^2}\right)}\)
Quelles sont les implications pratiques de la différence entre les deux formules ?
- Parce que l’intervalle de prédiction comporte le terme MSE supplémentaire, un intervalle de confiance \( \left( 1-\alpha \right) 100\% \) pour \(\mu_{Y}\) à \(x_{h}\) sera toujours plus étroit que l’intervalle de prédiction correspondant \( \left( 1-\alpha \right) 100\% \) pour \(y_{new}\) à \(x_{h}\).
- En calculant l’intervalle à la moyenne de l’échantillon des valeurs de prédiction \(\left(x_{h} = \bar{x}\right)\) et en augmentant la taille de l’échantillon n, l’erreur standard de l’intervalle de confiance peut s’approcher de 0. Comme l’intervalle de prédiction a le terme MSE supplémentaire, l’erreur standard de l’intervalle de prédiction ne peut pas s’approcher de 0.
La première implication se voit le plus facilement en étudiant le tracé suivant pour notre exemple de mortalité par cancer de la peau :
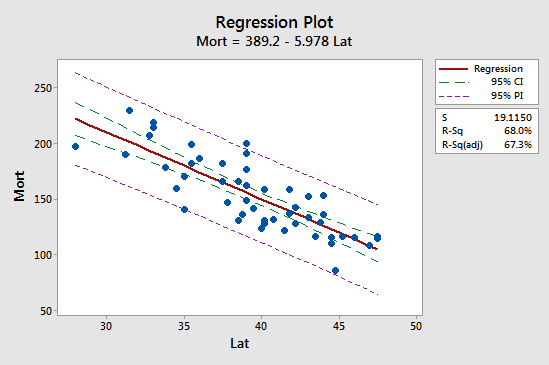
Observez que l’intervalle de prédiction (IP 95 %, en violet) est toujours plus large que l’intervalle de confiance (IC 95 %, en vert). De plus, les deux intervalles sont les plus étroits à la moyenne des valeurs prédictives (environ 39,5).