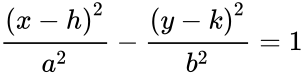by: adminPosted on:

Axe semi-majeur

File:Semimajoraxis.png

L’axe semi-majeur d’une ellipse

En géométrie, le terme axe semi-majeur (également axe semi-majeur) est utilisé pour décrire les dimensions des ellipses et des hyperboles.

Ellipse

Le grand axe d’une ellipse est son plus grand diamètre, une ligne qui passe par le centre et les deux foyers, ses extrémités étant aux points les plus larges de la forme. Le demi-grand axe est la moitié du grand axe, et va donc du centre, en passant par un foyer, jusqu’au bord de l’ellipse.

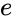
Il est relié au demi-petit axe {\displaystyle b\,\!} par l’excentricité {\displaystyle e\,\!} et le demi-petit axe.} et le rectum semi-latéral {\displaystyle \ell \,\ !}, comme suit :

{\displaystyle b=a{\sqrt {1-e^{2}}}\,\!}{\displaystyle \ell =a(1-e^{2})\,\!}{\displaystyle a\ell =b^{2}\,\!}.

Une parabole peut être obtenue comme la limite d’une séquence d’ellipses où un foyer est maintenu fixe alors que l’autre est autorisé à s’éloigner arbitrairement dans une direction, en gardant {\displaystyle \ell \,\!} fixe. Ainsi {\displaystyle a\,\!} et {\displaystyle b\,\!} tendent vers l’infini, {\displaystyle a\,\ !} plus rapidement que {\displaystyle b\,\!}.

Le demi-grand axe est la valeur moyenne des plus petites et plus grandes distances d’un foyer aux points de l’ellipse. Considérons maintenant l’équation en coordonnées polaires, avec un foyer à l’origine et l’autre sur l’axe x positif,

{\displaystyle r(1-e\cos \theta )=l\,\ !}

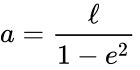
The mean value of {\displaystyle r={\ell \over {1+e}}\,\!} and {\displaystyle r={\ell \over {1-e}}\,\!}, is {\displaystyle a={\ell \over {1-e^{2}}}\,\!}.

Hyperbola

The semi-major axis of a hyperbola is one half of the distance between the two branches; if this is a in the x-direction the equation is:

{\displaystyle {\frac {\left(x-h\right)^{2}}{a^{2}}}-{\frac {\left(y-k\right)^{2}}{b^{2}}}=1}

In terms of the semi-latus rectum and the eccentricity we have

{\displaystyle a={\ell \over e^{2}-1}}

Astronomy

Orbital period

In astrodynamics the orbital period 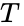{\displaystyle T\,} of a small body orbiting a central body in a circular or elliptical orbit is:

{\displaystyle T=2\pi {\sqrt {a^{3}/\mu }}}

where:

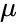
{\displaystyle a\,}est la longueur du demi-axe majeur de l’orbite{\displaystyle \mu }est le paramètre gravitationnel standard

Notez que pour toutes les ellipses ayant un demi-axe majeur donné, la période orbitale est la même, quelle que soit l’excentricité.

En astronomie, le demi-grand axe est l’un des éléments les plus importants d’une orbite, avec sa période orbitale. Pour les objets du système solaire, le demi-axe majeur est relié à la période de l’orbite par la troisième loi de Kepler (initialement dérivée empiriquement),

{\displaystyle T^{2}=a^{3}\,}

où T est la période en années, et a est le demi-axe majeur en unités astronomiques. Cette forme s’avère être une simplification de la forme générale du problème à deux corps, telle que déterminée par Newton :

{\displaystyle T^{2}={\frac {4\pi ^{2}}{G(M+m)}}a^{3}\,}

où G est la constante gravitationnelle, et M est la masse du corps central, et m est la masse du corps en orbite. Typiquement, la masse du corps central est tellement plus grande que celle du corps en orbite, que m peut être ignoré. En faisant cette hypothèse et en utilisant les unités typiques de l’astronomie, on obtient la forme plus simple que Kepler a découverte.

De façon remarquable, la trajectoire du corps en orbite autour du barycentre et sa trajectoire par rapport à son primaire sont toutes deux des ellipses. Le demi-axe majeur utilisé en astronomie est toujours la distance primaire-secondaire ; ainsi, les paramètres orbitaux des planètes sont donnés en termes héliocentriques. La différence entre les orbites primocentriques et les orbites « absolues » peut être illustrée au mieux en examinant le système Terre-Lune. Dans ce cas, le rapport de masse est de 81,30059. La distance caractéristique Terre-Lune, le demi-grand axe de l’orbite lunaire géocentrique, est de 384 400 km. L’orbite lunaire barycentrique, quant à elle, a un demi-grand axe de 379 700 km, la contre-orbite de la Terre prenant la différence, soit 4 700 km. La vitesse orbitale barycentrique moyenne de la Lune est de 1,010 km/s, tandis que celle de la Terre est de 0,012 km/s. Le total de ces vitesses donne la vitesse orbitale moyenne lunaire géocentrique, 1,022 km/s ; la même valeur peut être obtenue en considérant uniquement la valeur du demi-grand axe géocentrique.

Distance moyenne

On dit souvent que le demi-grand axe est la distance « moyenne » entre le primaire (le foyer de l’ellipse) et le corps en orbite. Ce n’est pas tout à fait exact, car cela dépend sur quoi la moyenne est prise.

  • La moyenne de la distance sur l’anomalie excentrique (q.v.) donne en effet l’axe semi-majeur.
  • La moyenne sur l’anomalie vraie (l’angle orbital vrai, mesuré au foyer) aboutit, bizarrement, à l’axe semi-minor {\displaystyle b=a{\sqrt {1-e^{2}}}\,\ !}.
  • La moyenne sur l’anomalie moyenne (la fraction de la période orbitale qui s’est écoulée depuis le péricentre, exprimée en angle), enfin, donne la moyenne temporelle (qui est ce que « moyenne » signifie généralement pour le profane) : {\displaystyle a(1+{\frac {e^{2}}{2}})\,\!}.

La moyenne temporelle de l’inverse du rayon, {\displaystyle r^{-1}\,\!}, est {\displaystyle a^{-1}\,\!}.

Énergie ; calcul du demi-axe majeur à partir des vecteurs d’état

En astrodynamique, le demi-axe majeur {\displaystyle a\,} peut être calculé à partir des vecteurs d’état orbitaux :

{\displaystyle a={-\mu \over {2\epsilon }}\,} for an elliptical orbit and {\displaystyle a={\mu \over {2\epsilon }}\,} for a hyperbolic trajectory

and

{\displaystyle \epsilon ={v^{2} \over {2}}-{\mu \over \left|\mathbf {r} \right|}} (specific orbital energy)

and

{\displaystyle \mu =GM\,} (standard gravitational parameter),

where:

  • {\displaystyle v\,} is orbital velocity from velocity vector of an orbiting object,
  • {\displaystyle \mathbf {r} \,} is cartesian position vector of an orbiting object in coordinates of a reference frame with respect to which the elements of the orbit are to be calculated (e.g. équatoriale géocentrique pour une orbite autour de la Terre, ou écliptique héliocentrique pour une orbite autour du Soleil),
  • {\displaystyle G\,} est la constante gravitationnelle,
  • {\displaystyle M\,} la masse du corps central.

Notez que pour un corps central et une énergie spécifique totale donnés, le demi-grand axe est toujours le même, quelle que soit l’excentricité. Inversement, pour un corps central et un demi-axe majeur donnés, l’énergie spécifique totale est toujours la même.

Exemple

La station spatiale internationale a une période orbitale de 91,74 minutes, donc le demi-axe majeur est de 6738 km . Chaque minute de plus correspond à environ 50 km de plus : les 300 km supplémentaires de longueur d’orbite prennent 40 secondes, la baisse de vitesse compte pour 20 secondes supplémentaires.

.

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *