Dans cette section, nous allons apprendre à trouver la ou les racines d’une équation quadratique. Les racines sont également appelées » x-intercepts » ou » zéros « . Une fonction quadratique est représentée graphiquement par une parabole dont le sommet est situé à l’origine, sous l’axe des x ou au-dessus de l’axe des x. Par conséquent, une fonction quadratique peut avoir une, deux ou zéro racine.
Quand on nous demande de résoudre une équation quadratique, on nous demande en réalité de trouver les racines. Nous avons déjà vu que compléter le carré est une méthode utile pour résoudre les équations quadratiques. Cette méthode peut être utilisée pour dériver la formule quadratique, qui est utilisée pour résoudre les équations quadratiques. En fait, les racines de la fonction,
f (x) = ax2 + bx + c
sont données par la formule quadratique. Les racines d’une fonction sont les ordonnées en x. Par définition, la coordonnée y des points situés sur l’axe des x est nulle. Par conséquent, pour trouver les racines d’une fonction quadratique, nous définissons f (x) = 0, et résolvons l’équation,
ax2 + bx + c = 0.
We can do this by completing the square as,
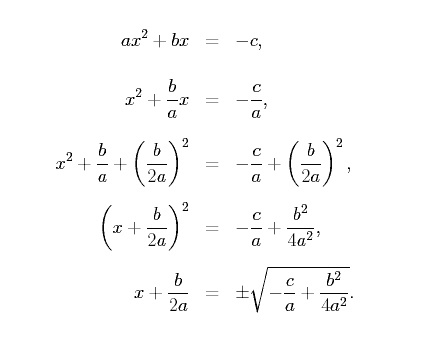
Solving for x and simplifying we have,
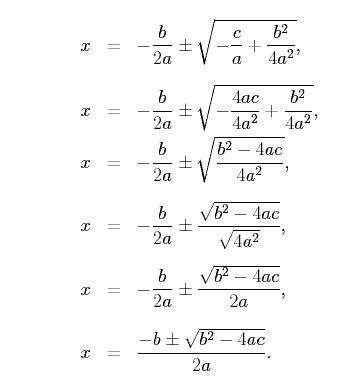
Thus, the roots of a quadratic function are given by,
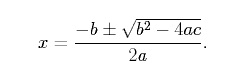
This formula is called the quadratic formula, and its derivation is included so that you can see where it comes from. We call the term b2 −4ac the discriminant. The discriminant is important because it tells you how many roots a quadratic function has. Specifically, if
1. b2 −4ac < 0 There are no real roots.
2. b2 −4ac = 0 There is one real root.
3. b2 −4ac > 0 There are two real roots.
We will examine each case individually.
Cas 1 : pas de racines réelles
Si le discriminant d’une fonction quadratique est inférieur à zéro, cette fonction n’a pas de racines réelles et la parabole qu’elle représente ne coupe pas l’axe des x. Comme la formule quadratique exige de prendre la racine carrée du discriminant, un discriminant négatif crée un problème car la racine carrée d’un nombre négatif n’est pas définie sur la ligne réelle. Un exemple de fonction quadratique sans racines réelles est donné par,
f(x) = x2 – 3x + 4.
Notez que le discriminant de f(x) est négatif,
b2 -4ac = (-3)2- 4 – 1 – 4 = 9 – 16 = -7.
Cette fonction est représentée graphiquement par une parabole qui s’ouvre vers le haut dont le sommet se trouve au-dessus de l’axe des x. Ainsi, le graphe ne peut jamais couper l’axe des x et n’a pas de racines, comme le montre le graphique ci-dessous,
Cas 2 : une racine réelle
Si le discriminant d’une fonction quadratique est égal à zéro, cette fonction a exactement une racine réelle et croise l’axe des x en un seul point. Pour voir cela, on met b2 -4ac = 0 dans la formule quadratique pour obtenir,
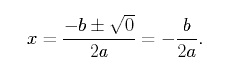
Remarquez que 
est la coordonnée x du sommet d’une parabole. Ainsi, une parabole a exactement une racine réelle lorsque le sommet de la parabole se trouve juste sur l’axe des x. L’exemple le plus simple d’une fonction quadratique qui a une seule racine réelle est,
y = x2,
où la racine réelle est x = 0.
Un autre exemple de fonction quadratique avec une racine réelle est donné par,
f(x) = -4×2 + 12x – 9.
Notez que le discriminant de f(x) est nul,
b2 -4ac = (12)2- 4 – -4 – -9 = 144 – 144 = 0.
Cette fonction est représentée graphiquement par une parabole qui s’ouvre vers le bas et dont le sommet (3/2, 0) est situé sur l’axe des x. Thus, the graph intersects the x-axis at exactly one point (i.e. has one root) as shown below,
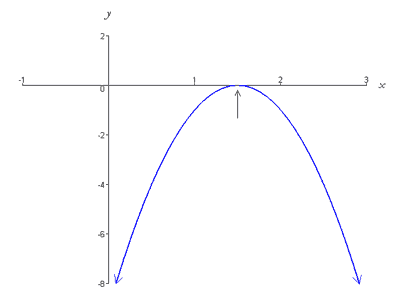
Case 3: Two Real Roots
If the discriminant of a quadratic function is greater than zero, that function has two real roots (x-intercepts). Taking the square root of a positive real number is well defined, and the two roots are given by,
An example of a quadratic function with two real roots is given by,
f(x) = 2×2− 11x + 5.
Notice that the discriminant of f(x) is greater than zero,