Une fonction de production Cobb-Douglas modélise la relation entre la production et les intrants de production (facteurs). Elle est utilisée pour calculer les ratios des intrants entre eux pour une production efficace et pour estimer le changement technologique dans les méthodes de production. L’application de cette forme fonctionnelle à la mesure de la production est due au mathématicien Charles Cobb et à l’économiste Paul Douglas qui l’ont utilisée pour étudier l’importance relative des deux facteurs d’entrée, le travail et le capital, dans la production manufacturière aux États-Unis sur la période 1899 à 1922. Dans leur modèle original, Cobb et Douglas limitent les paramètres d’élasticité de la production \(\alpha_{1}\) et \(\alpha_{2}\) à l’intervalle \(\alpha_{i}\in\left(0,1\right)\) et à une somme égale à un, ce qui implique des rendements d’échelle constants. La fonction est donc \ où \(x_{1}\) et \(x_{2}\) représentent respectivement le travail et le capital. En prenant le logarithme naturel des deux côtés de l’équation, on obtient un rendement tel que, pour des données sur la production, le travail et le capital, les paramètres \(\gamma\) et \(\alpha_{1}\) peuvent être estimés à l’aide des moindres carrés ordinaires. Sur la base de leurs données, Cobb et Douglas trouvent une valeur de 0,75 pour \(\alpha_{1}\), ce qui implique que le travail a représenté les trois quarts de la valeur de la production manufacturière américaine (le capital représentant le quart restant) au cours de la période étudiée. Leur estimation du paramètre d’efficacité \(\gamma\) est de 1,01 qui, étant supérieur à 1, reflète les effets positifs des forces inobservables sur la production par la combinaison du travail et du capital.
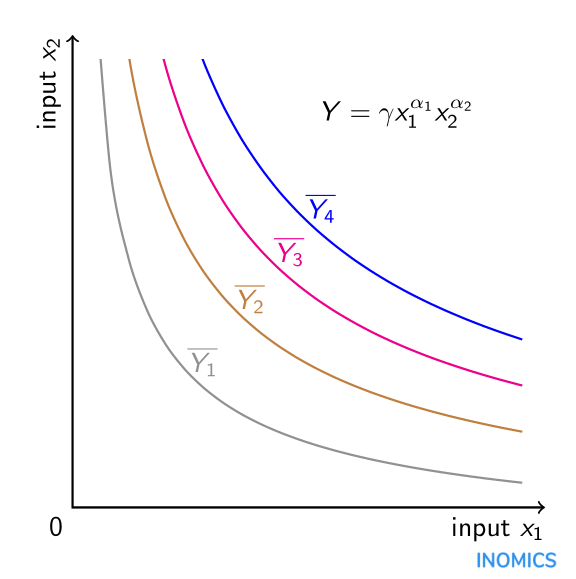
Le caractère multiplicatif d’une fonction de production Cobb-Douglas, supposant des valeurs positives pour \(\alpha_{i}\), signifie que les intrants sont complémentaires dans la production. Dans le modèle standard du travail et du capital, l’augmentation de la quantité de capital accroît la production non seulement directement, mais aussi indirectement par son impact sur la productivité du travail. Mathématiquement, la dérivée croisée partielle de la production \(Y\) par rapport au travail \(x_{1}\) et au capital \(x_{2}\) est positive. En outre, en raison de l’hypothèse selon laquelle \(\alpha_{i}\in\left(0,1\right)\), les dérivées partielles de second ordre de la production par rapport au travail et par rapport au capital sont toutes deux négatives, ce qui implique des rendements marginaux décroissants pour chaque intrant uniquement. Le simple fait d’ajouter soit plus de travail, soit plus de capital (mais pas les deux) au processus de production augmente la production, mais à un rythme décroissant. En outre, l’élasticité de substitution entre les intrants est constante et égale à un en raison de la forme fonctionnelle. Une fonction de production Cobb-Douglas à deux entrées peut être représentée graphiquement sous la forme d’isoquantes : combinaisons des deux entrées pour lesquelles la production est constante. Il existe quatre isoquantes de ce type dans le graphique ci-dessus pour les niveaux de production (constants) : \(\overline{Y_{1}}\), \(\overline{Y_{2}}\), \(\overline{Y_{3}}\) et \(\overline{Y_{4}}\). Plus l’isoquant est éloigné de l’origine, plus le niveau de production est élevé \(\overline{Y_{4}}>\overline{Y_{3}>\overline{Y_{2}>\overline{Y_{1}}\). La combinaison précise des intrants \(x_{1}\) et \(x_{2}\) qui est optimale pour la production est déterminée par le budget dont dispose le producteur ainsi que par le rapport de coût de l’intrant \(x_{2}\) sur l’intrant \(x_{1}\) qui peut être inclus dans le graphique sous la forme d’une ligne d’isocoût (voir l’article sur l’élasticité de substitution).
Cobb et Douglas ont eux-mêmes reconnu que leur fonction de production ne repose pas sur des fondements théoriques solides et qu’elle ne doit pas non plus être comprise comme une loi de la production ; elle représente simplement une approximation statistique des relations observées entre les facteurs de production et la production. Néanmoins, ses propriétés mathématiques simples sont attrayantes pour les économistes et l’ont conduit à devenir un standard de la théorie microéconomique au cours du siècle dernier.
Lecture complémentaire:
Pour le contexte et un aperçu des principales propriétés des fonctions de production Cobb-Douglas, voir notamment les sections 6, 7 et 8 de l’article original de Cobb et Douglas, « A Theory of Production » (The American Economic Review, 1928).
Bon à savoir :
La forme fonctionnelle de Cobb-Douglas n’est pas seulement utilisée dans la théorie de la production mais elle est également devenue standard dans la théorie microéconomique du consommateur où elle est appliquée comme fonction d’utilité, où \(Y\) devient \(U\) pour l’utilité. Les \(x_{i}\) représentent alors les articles de consommation et, lorsque la fonction d’utilité est maximisée sous réserve d’une contrainte budgétaire, les valeurs de \(\alpha_{i}\) indiquent comment l’individu répartira de manière optimale son budget entre les articles.